题目内容
甲、乙、丙三人在同一条公路上,甲在乙丙之间的丁字路口上,丙在西,乙在东,乙丙之间相距700米,乙丙二人同时相向而行,丙每分钟走60米,经过5分钟两人相遇,这时乙超过丁字路口80米,当乙丙相遇时,甲立即向南而行,乙立即返回并经过丁字口向南而行.丙每分钟比甲少行10米,问甲出发后几分钟乙可以追上甲?
分析:根据题干,此题可分为两部分进行讨分析:(1)乙丙相遇问题:如下图分析,可设乙的速度为x米\分,根据甲行驶的路程+乙行驶的路程=总路程700米,可以列出方程解决问题.
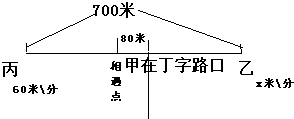
(2)乙与甲的追及问题:如下图分析,此时甲乙相距80米,甲的速度为60+10=70米\分,设经过y分钟乙追上甲,根据乙行驶的路程-甲行驶的路程=80米,列出方程,即可解决问题.

(2)乙与甲的追及问题:如下图分析,此时甲乙相距80米,甲的速度为60+10=70米\分,设经过y分钟乙追上甲,根据乙行驶的路程-甲行驶的路程=80米,列出方程,即可解决问题.

解答:解:(1)设乙的速度为x米\分,根据题意可得方程:
60×5+5x=700,
解得x=80,
(2)设经过y分钟后乙追上甲,根据题意可得方程:
80y-(60+10)y=80,
解得y=8,
答:甲出发后,经过8分钟乙追上甲.
60×5+5x=700,
解得x=80,
(2)设经过y分钟后乙追上甲,根据题意可得方程:
80y-(60+10)y=80,
解得y=8,
答:甲出发后,经过8分钟乙追上甲.
点评:此题考查了相遇问题与追及问题的综合运用的方法.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目