题目内容
将自然数按下面的规律分组:(1,2),(3,4,5,6),(7,8,9,10,11,12),(13,14,15,16,17,18,19,
20),…,第1991组的第一个数和最后一个数各是
20),…,第1991组的第一个数和最后一个数各是
3962091
3962091
3966072
3966072
.分析:每一组数的个数都在增加,第n组数的个数为2n个数,这组的第一个数就是前一组数的最后一个数+1,这个数是2+4+6+…+2(n-1)+1;当然,这组数的最后一个数是2+4+6+…+2n;当n=1991时,代入1991可得解.
解答:解:2+4+6+…+2(1991-1)+1
=2(1+2+3+…+1990)+1
=(1+1990)×1990+1
=3962091;
2+4+6+…+2×1991
=2×(1+2+3+…+1991)
=(1+1991)×1991
=3966072;
答:第1991组的第一个数和最后一个数各是3962091、3966072;
故答案为:3962091,3966072.
=2(1+2+3+…+1990)+1
=(1+1990)×1990+1
=3962091;
2+4+6+…+2×1991
=2×(1+2+3+…+1991)
=(1+1991)×1991
=3966072;
答:第1991组的第一个数和最后一个数各是3962091、3966072;
故答案为:3962091,3966072.
点评:此题考查了数表中的规律,每一组数的个数为组数的2倍,正整数依次填入,发现规律,解决问题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 (a是大于0的自然数)的大小吗?答:______
(a是大于0的自然数)的大小吗?答:______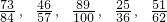 .______
.______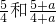 (a是大于0的自然数)为例,验证你的猜想,说一说,与上面的规律有什么不同?
(a是大于0的自然数)为例,验证你的猜想,说一说,与上面的规律有什么不同?