题目内容
19.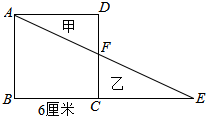 在图中,正方形ABCD的边长是6cm,三角形乙的面积比三角形甲大6cm
在图中,正方形ABCD的边长是6cm,三角形乙的面积比三角形甲大6cm2,CE的长度是多少厘米.
分析 根据三角形乙的面积比三角形甲大6cm2,则根据图形可得:三角形ABE的面积比正方形ABCD的面积大6平方厘米.由此可得三角形ABE的面积等于正方形的面积加上6平方厘米,求得三角形ABE的面积后,再利用三角形的面积公式求出BE的长后即可求得CE的长.
解答 解:三角形甲的面积比三角形乙的面积小6平方厘米;
根据图形可得:三角形ABE的面积比正方形ABCD的面积大6平方厘米,
所以三角形ABE的面积为:6×6+6=42(平方厘米),
又因为正方形的边长AB=6厘米,
所以EB的长度是:42×2÷6=14(厘米),
所以CE的长度为:14-6=8(厘米),
答:CE的长度是8厘米.
点评 此题考查了三角形和正方形面积公式的灵活应用,这里根据题干得出三角形与正方形的面积之差是6平方厘米是解决问题的关键.

练习册系列答案
相关题目
3.直接写出得数
| 1.2+8 | 24-18 | 30×60 | 540÷90 |
| $\frac{1}{4}$+2 | $\frac{4}{5}$×$\frac{3}{4}$ | $\frac{6}{9}$$÷\frac{6}{9}$ | $\frac{1}{3}$-$\frac{1}{5}$ |
| $\frac{7}{10}$×$\frac{1}{2}$ | $\frac{4}{15}$÷2 | $\frac{7}{18}$×$\frac{1}{14}$ | 8÷$\frac{4}{5}$ |
| $\frac{4}{15}$×$\frac{5}{8}$ | 2×$\frac{9}{20}$ | $\frac{3}{5}$÷$\frac{2}{3}$ | 15÷$\frac{1}{5}$ |