题目内容
我们已经知道三角形三个内角度数的和是180°.
(1)你能运用这个知识求出四边形、五边形、六边形等多边形的内角和吗?你能把想法用图表示出来吗?
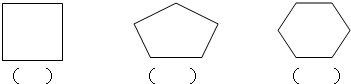
你仔细思考后发现了什么规律?试一试用自己的话说出来.
(2)请你用字母的式子表示出n边形内角和. .
(1)你能运用这个知识求出四边形、五边形、六边形等多边形的内角和吗?你能把想法用图表示出来吗?

你仔细思考后发现了什么规律?试一试用自己的话说出来.
(2)请你用字母的式子表示出n边形内角和.
分析:根据过同一顶点作出的对角线把多边形分成的三角形的个数的规律,再利用三角形的内角和等于180°即可推出多边形的内角和公式.
解答:解:(1)
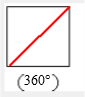
四边形分成2个三角形;
180°×2=360°;
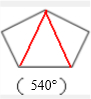
五边形分成3个三角形;
180°×3=540°;
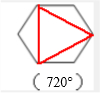
六边形分成4个三角形:
180°×4=720°
规律:多边形每增加一个边,内角和就增加180°;
(2)n边形的内角和可以表示为:(n-2)?180°.
故答案为:(n-2)?180°.

四边形分成2个三角形;
180°×2=360°;

五边形分成3个三角形;
180°×3=540°;

六边形分成4个三角形:
180°×4=720°
规律:多边形每增加一个边,内角和就增加180°;
(2)n边形的内角和可以表示为:(n-2)?180°.
故答案为:(n-2)?180°.
点评:本题考查了多边形的内角和公式的推导,理清过同一个顶点把多边形分成的三角形的个数是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


