题目内容
有长度分别是1厘米、2厘米、3厘米、4厘米、5厘米、6厘米、7厘米、8厘米、9厘米的小木棒各一根,从中选择若干根小木棒拼成一个正方形(不许折断),一共有多少种不同的拼法?请画出其中的四种拼法,标出小棒的长度.
分析:根据正方形的周长公式可得,正方形的周长是4的倍数,将1+2+…+9=45,那么拼成的正方形的周长应是小于45厘米的4的倍数,经讨论可以确定能拼出的正方形的边长.
解答:解:1+2+…+9=45,
小于45的4的倍数有,4,8,12,16,20,24,28,32,36,40,44,
所以相对应的正方形的边长应为1厘米,2厘米,3厘米,4厘米,5厘米,6厘米,7厘米,8厘米,9厘米,10厘米,11厘米.
根据题意分析可得,利用题干中的小棒能拼出的正方形只有边长为7厘米;8厘米;9厘米;10厘米,11厘米,
边长7厘米:7、1+6、2+5、3+4 可组成一种正方形
边长8:8、1+7、2+6、3+5 可组成一种正方形
边长9:9、1+8、2+7、3+6、4+5 可组成五种正方形
边长10:1+9、2+8、3+7、4+6 可组成一种正方形
边长11:2+9、3+8、4+7、5+6 可组成一种正方形
一共可组成9种.
答:共有9种拼法.
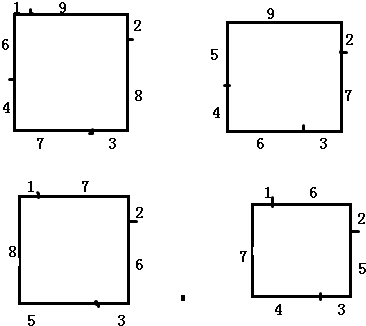
拼法如下图所示:
小于45的4的倍数有,4,8,12,16,20,24,28,32,36,40,44,
所以相对应的正方形的边长应为1厘米,2厘米,3厘米,4厘米,5厘米,6厘米,7厘米,8厘米,9厘米,10厘米,11厘米.
根据题意分析可得,利用题干中的小棒能拼出的正方形只有边长为7厘米;8厘米;9厘米;10厘米,11厘米,
边长7厘米:7、1+6、2+5、3+4 可组成一种正方形
边长8:8、1+7、2+6、3+5 可组成一种正方形
边长9:9、1+8、2+7、3+6、4+5 可组成五种正方形
边长10:1+9、2+8、3+7、4+6 可组成一种正方形
边长11:2+9、3+8、4+7、5+6 可组成一种正方形
一共可组成9种.
答:共有9种拼法.
拼法如下图所示:

点评:利用正方形的周长来确定所拼成的正方形的边长,是解决本题的关键.

练习册系列答案
相关题目