题目内容
 如图,三角形ABC和三角形DEF分别是等腰直角三角形.已知DF=6,AB=5,EB=2.6,则阴影部分的面积是
如图,三角形ABC和三角形DEF分别是等腰直角三角形.已知DF=6,AB=5,EB=2.6,则阴影部分的面积是9.78
9.78
.分析:因为△ABC和△DEF都是等腰三角形,所以有EF=DF=6,BC=AB=5,又因为∠E=∠C=45°,所以∠EHC=90°,由此∠AGH=45°,又∠EGB=∠AGH=45°,因此,三角形EBG也是等腰直角三角形,同理三角形AGH、EIC都是等腰直角三角形,有EB=BG=2.6,AG=2.4,由此可以求阴影部分的面积.
解答:解:S△AGH=
×2.4×2.4×
=1.44;
又因为BF=EF-EB=3.4,所以FC=BC-BF=5-3.4=1.6;
S△FCI=
×1.6×1.6=1.28;
所以阴影的面积为:
S阴影=S△ABC-S△AGH-S△FCI
=
×5×5-1.44-1.28
=12.5-1.44-1.28
=9.78;
答:阴影部分的面积是9.78.
故此题答案为:9.78.
| 1 |
| 2 |
| 1 |
| 2 |
又因为BF=EF-EB=3.4,所以FC=BC-BF=5-3.4=1.6;
S△FCI=
| 1 |
| 2 |
所以阴影的面积为:
S阴影=S△ABC-S△AGH-S△FCI
=
| 1 |
| 2 |
=12.5-1.44-1.28
=9.78;
答:阴影部分的面积是9.78.
故此题答案为:9.78.
点评:此题主要考查等腰直角三角形的特点,进行合理的图形拼组是解决此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
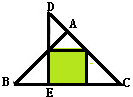 (2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是
(2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是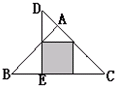 如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是
如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是 (2007?淮安模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC和三角形DEC的面积比是( )
(2007?淮安模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC和三角形DEC的面积比是( ) 如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是________平方米.
如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是________平方米.