题目内容
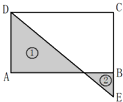 长方形ABCD的长是10厘米,宽是6厘米,阴影部分①的面积比阴影部分②的面积大0.2平方分米.求BE的长度是多少厘米?
长方形ABCD的长是10厘米,宽是6厘米,阴影部分①的面积比阴影部分②的面积大0.2平方分米.求BE的长度是多少厘米?
解:0.2平方分米=20平方厘米;
长方形的面积=10×6=60(平方厘米);
因为①的面积比②的面积多20平方厘米;
所以三角形CDE的面积=60-20=40(平方厘米);
CE=40×2÷10=8(厘米);
BE=8-6=2(厘米);
答:BE的长度是2厘米.
分析:根据题意可知,阴影部分①的面积比阴影部分②的面积大0.2平方分米(20平方厘米),也就是长方形ABCD的面积比三角形ECD的面积大20平方厘米,那么长方形的面积减去20平方厘米即是三角形ECD的面积.然后根据三角形的面积公式逆算出CE边的长,再减去BC就是BE的长;由此解答.
点评:此题解答关键是通过转化,将图中①比②大20平方厘米,转化为长方形ABCD的面积比三角形ECD的面积大20平方厘米,然后根据三角形的面积计算方法解决问题.
长方形的面积=10×6=60(平方厘米);
因为①的面积比②的面积多20平方厘米;
所以三角形CDE的面积=60-20=40(平方厘米);
CE=40×2÷10=8(厘米);
BE=8-6=2(厘米);
答:BE的长度是2厘米.
分析:根据题意可知,阴影部分①的面积比阴影部分②的面积大0.2平方分米(20平方厘米),也就是长方形ABCD的面积比三角形ECD的面积大20平方厘米,那么长方形的面积减去20平方厘米即是三角形ECD的面积.然后根据三角形的面积公式逆算出CE边的长,再减去BC就是BE的长;由此解答.
点评:此题解答关键是通过转化,将图中①比②大20平方厘米,转化为长方形ABCD的面积比三角形ECD的面积大20平方厘米,然后根据三角形的面积计算方法解决问题.

练习册系列答案
相关题目
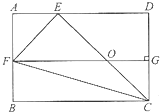 如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,求OG长多少厘米?
如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,求OG长多少厘米? 长方形ABCD的长是10厘米,宽是6厘米,阴影部分①的面积比阴影部分②的面积大0.2平方分米.求BE的长度是多少厘米?
长方形ABCD的长是10厘米,宽是6厘米,阴影部分①的面积比阴影部分②的面积大0.2平方分米.求BE的长度是多少厘米? 长方形ABCD的长是4厘米、宽3厘米.从这个长方形中剪去两个长2厘米、宽1厘米的小长方形后得到一个“T”形(如图).请你沿直线(用虚线在图上画出这样的直线)把这个“T”形剪两刀,并使剪开的部分恰好能拼成一个正方形.
长方形ABCD的长是4厘米、宽3厘米.从这个长方形中剪去两个长2厘米、宽1厘米的小长方形后得到一个“T”形(如图).请你沿直线(用虚线在图上画出这样的直线)把这个“T”形剪两刀,并使剪开的部分恰好能拼成一个正方形.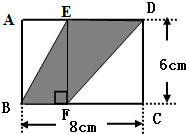 长方形ABCD的长是8cm,宽是6cm(如图).求阴影部分的面积.
长方形ABCD的长是8cm,宽是6cm(如图).求阴影部分的面积.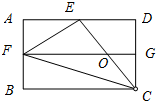 如图,长方形ABCD的长是12厘米,宽是8厘米,FG与BC平行,OG长是4厘米.三角形CEF的面积是
如图,长方形ABCD的长是12厘米,宽是8厘米,FG与BC平行,OG长是4厘米.三角形CEF的面积是