题目内容
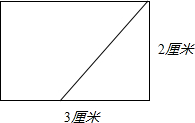
 如图是一个长3厘米、宽2厘米的长方形.
如图是一个长3厘米、宽2厘米的长方形.(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.
(2)其中梯形的面积是
4
4
平方厘米.(3)以梯形的最短边所在的直线为轴,将它高速旋转,旋转时形成图形的体积是
28
28
立方厘米.(π的值取“3”计算.)分析:(1)从长边的3厘米中量出2厘米的点,再与下角画一条线段,就成一个等腰直角三角形和一个梯形;
(2)将数据代入梯形面积公式,即可求出梯形的面积;
(3)以梯形的最短边所在的直线为轴,将为轴,将梯形高速旋转,形成的图形的体积是底面半径2厘米,高3厘米的圆柱的体积-底面半径2厘米、高2厘米的圆锥的体积,据此计算即可.
(2)将数据代入梯形面积公式,即可求出梯形的面积;
(3)以梯形的最短边所在的直线为轴,将为轴,将梯形高速旋转,形成的图形的体积是底面半径2厘米,高3厘米的圆柱的体积-底面半径2厘米、高2厘米的圆锥的体积,据此计算即可.
解答:解:(1)所作的等腰直角三角形的直角边是2厘米,梯形的上底是1厘米,下底是3厘米,高是2厘米;
(2)梯形的面积=(3-2+3)×2÷2,
=4×2÷2,
=4(平方厘米);
答:梯形的面积是4平方厘米.
(3)3×22×3-
×3×22×2,
=36-8,
=28(立方厘米),
答:这个图形的体积是28立方厘米.
故答案为:4;28.

(2)梯形的面积=(3-2+3)×2÷2,
=4×2÷2,
=4(平方厘米);
答:梯形的面积是4平方厘米.
(3)3×22×3-
| 1 |
| 3 |
=36-8,
=28(立方厘米),
答:这个图形的体积是28立方厘米.
故答案为:4;28.
点评:此题主要考查梯形面积公式及圆柱与圆锥的体积公式,关键是找清旋转后的图形中,圆柱与圆锥的底面半径和高,将数据代入公式即可求得结果.

练习册系列答案
相关题目
 (2012?瑶海区)如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的表面积( )
(2012?瑶海区)如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的表面积( )
 (2011?苏州模拟)如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的体积是
(2011?苏州模拟)如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的体积是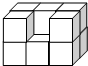 (2012?陆良县)如图是一个长3厘米,宽与高都是2厘米的长方体,在它的上面挖掉一个棱长为1厘米的小正方体,这时它的表面积是( )平方厘米.
(2012?陆良县)如图是一个长3厘米,宽与高都是2厘米的长方体,在它的上面挖掉一个棱长为1厘米的小正方体,这时它的表面积是( )平方厘米.