题目内容
5．
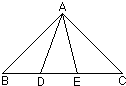如图，△ABC中，AB=AC，∠ABC=36°，D、E是BC上的点，∠BAD=∠DAE=∠EAC，则图中等腰三角形的个数是6个．
分析 根据△ABC中，AB=AC，∠ABC=36°，D、E是BC上的点，∠BAD=∠DAE=∠EAC这些条件，再根据三角形的内角和是180°和等腰三角形的性质，求出各个角的度数，即可判断哪些角是等腰三角形．
解答 解：因为在△ABC中，AB=AC，所以△ABC是等腰三角形，
因为∠BAD=∠DAE=∠EAC=（180°-36°-36°）÷3=36°，所以△ABD、△ADE、△AEC是等腰三角形，
又因为∠BAE=∠CAD=36°+36°=72°，∠BEA=∠CDA=180°-72°-36°=72°，所以∠BAE=∠CAD=∠BEA=∠CDA=72°，
所以△BAE、△CAD是等腰三角形，一共有6个．
点评 本题考查了三角形的特性，要把所有的图形情况都考虑清楚，看看哪两条边相等．
练习册系列答案
相关题目
（1）画出三角形BC边上的高．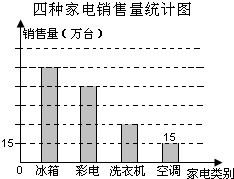
近日从省家电下乡联席办获悉，自2012年2月20日我省家电下乡全面启动以来，最受农户热捧的四种家电是冰箱、彩电、洗衣机和空调，其销售量比是5：4：2：1，其中空调已销售了15万台，根据上述销售情况绘制了一个不完整的统计图：