题目内容
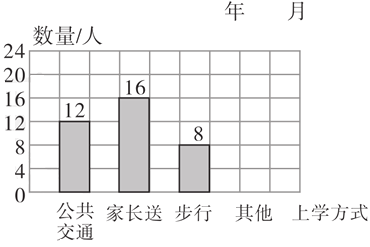
【题目】在下面的长方形ABCD中,三角形BEO的面积是1平方厘米,三角形ABO的面积是3平方平方厘米,则长方形ABCD的面积是(________)平方厘米。

【答案】24
【解析】
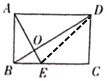
连接DE。三角形ABE与三角形DBE同底等高,则它们的面积相等。从这两个三角形中分别减去三角形BEO,则剩下的图形面积相等,即三角形ABO与三角形DEO的面积相等。在三角形DBE中,三角形BEO与三角形DEO的高相等,面积比是1∶3,则它们的底的比也是1∶3,即BO∶OD=1∶3;在三角形ABD中,三角形ABO与三角形ADO的高相等,底的比是1∶3,则它们的面积比也是1∶3,三角形ADO的面积为3×3=9(平方厘米)。长方形ABCD的面积相当于是三角形ABO与三角形ADO面积和的2倍。
长方形ABCD的面积:(三角形ABO的面积+三角形ADO的面积)×2
=(3+9)×2
=12×2
=24(平方厘米)
即长方形ABCD的面积是24平方厘米。

练习册系列答案
相关题目
【题目】下面的统计图和统计表记录了小林家上月部分费用的支出情况。请把表格填写完整。
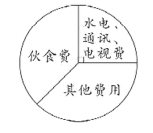
支出项目 | 所占百分比 | 支出金额/元 |
合计 | (________) | 1500 |
水电、通讯、电视费 | (________) | (________) |
伙食费 |
| (________) |
其他费用 | (________) | (________) |