题目内容
扇形的半径扩大为原来的2倍,圆心角缩小为原来的 ,那么扇形的面积
,那么扇形的面积
- A.不变
- B.扩大为原来的2倍
- C.缩小为原来的

- D.扩大为原来的4倍
B
分析:扇形的面积=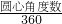 ×πr2,由此设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,由此利用扇形的面积公式即可计算得出它们的面积,从而进行比较选择.
×πr2,由此设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,由此利用扇形的面积公式即可计算得出它们的面积,从而进行比较选择.
解答:设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,根据扇形的面积公式可得:
原来扇形的面积为: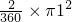 =
=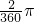 ;
;
变化后扇形面积为: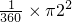 =
=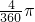 ;
;
原来扇形面积:变化后扇形面积=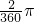 :
: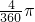 =1:2;
=1:2;
故选:B.
点评:此题考查了扇形面积公式的灵活应用.
分析:扇形的面积=
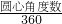 ×πr2,由此设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,由此利用扇形的面积公式即可计算得出它们的面积,从而进行比较选择.
×πr2,由此设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,由此利用扇形的面积公式即可计算得出它们的面积,从而进行比较选择.解答:设原来扇形的半径为1,圆心角为2°,则变化后的扇形的半径为2,圆心角为1°,根据扇形的面积公式可得:
原来扇形的面积为:
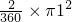 =
=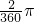 ;
;变化后扇形面积为:
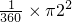 =
=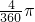 ;
;原来扇形面积:变化后扇形面积=
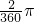 :
: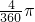 =1:2;
=1:2;故选:B.
点评:此题考查了扇形面积公式的灵活应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目