题目内容
6.计算下面各题,能简便计算的要简便计算.| $\frac{9}{8}$-$\frac{1}{7}$+$\frac{1}{8}$-$\frac{6}{7}$ | $\frac{11}{12}$-$\frac{1}{3}$+$\frac{1}{4}$ | $\frac{5}{9}$+$\frac{5}{6}$-($\frac{5}{6}$-$\frac{4}{9}$) |
| $\frac{1}{7}$-$\frac{1}{5}$+$\frac{6}{7}$-$\frac{4}{5}$ | $\frac{2}{3}$+$\frac{2}{9}$+$\frac{2}{27}$+$\frac{2}{81}$+$\frac{2}{243}$ |
分析 (1)、(3)、(4)根据加法交换律和结合律以及减法的性质进行简算;
(2)按照从左向右的顺序进行计算;
(5)每个分数的分子都是2,后一个分数的分母是前一个分数分母的3倍,于是把每个分数拆成两个分数相减的形式,然后通过加减相互抵消,求出结果.
解答 解:(1)$\frac{9}{8}$-$\frac{1}{7}$+$\frac{1}{8}$-$\frac{6}{7}$
=($\frac{9}{8}$+$\frac{1}{8}$)-($\frac{1}{7}$+$\frac{6}{7}$)
=$\frac{5}{4}$-1
=$\frac{1}{4}$;
(2)$\frac{11}{12}$-$\frac{1}{3}$+$\frac{1}{4}$
=$\frac{7}{12}$+$\frac{1}{4}$
=$\frac{5}{6}$;
(3)$\frac{5}{9}$+$\frac{5}{6}$-($\frac{5}{6}$-$\frac{4}{9}$)
=$\frac{5}{9}$+$\frac{5}{6}$-$\frac{5}{6}$+$\frac{4}{9}$
=($\frac{5}{9}$+$\frac{4}{9}$)+($\frac{5}{6}$-$\frac{5}{6}$)
=1+0
=1;
(4)$\frac{1}{7}$-$\frac{1}{5}$+$\frac{6}{7}$-$\frac{4}{5}$
=($\frac{1}{7}$+$\frac{6}{7}$)-($\frac{1}{5}$+$\frac{4}{5}$)
=1-1
=0;
(5)$\frac{2}{3}$+$\frac{2}{9}$+$\frac{2}{27}$+$\frac{2}{81}$+$\frac{2}{243}$
=(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{9}$)+($\frac{1}{9}$-$\frac{1}{27}$)+($\frac{1}{27}$-$\frac{1}{81}$)+($\frac{1}{81}$-$\frac{1}{243}$)
=1-$\frac{1}{243}$
=$\frac{242}{243}$.
点评 考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律简便计算.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | 40、16、0.8 | B. | 20、5、8 | C. | 20、32、8 |
| A. | 12和24 | B. | 15和51 | C. | 18和43 |
| A. | 2400 | B. | 3000 | C. | 4000 | D. | 2700 |
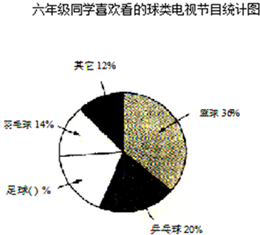 根据统计图完成下面各题.
根据统计图完成下面各题.