Question

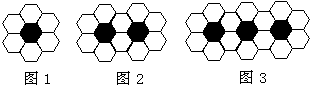用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案：
（1）第4个图案中有

18

块白色地砖；
（2）第2009个图案中有

8038

块白色地砖．

Answer 1

分析：通过观察，前三个图案中白色地砖的块数分别为：6，10，14，所以会发现后面的图案比它前面的图案多4块白色地砖，可得第n个图案有4n+2块白色地砖．

解答：解：结合图形，第一个图案有白色地砖6块，后边每多一个图案，则多4块白色地砖．
根据这个规律第n个图案中有白色地砖：4n+2块．
（1）当n=4时，4×4+2=18（块），
答：第4个图案中有18块白色地砖．

（2）当n=2009时，4×2009+2=8038块．
答：第2009个图案中有8038块地砖．
故答案为：18；8038．

点评：此类题要能够结合图形，发现规律：在第一个图案的基础上，多一个图案，多4块白色地砖．是解决本题的关键．