题目内容
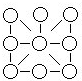如图，将| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 12 |
| 5 |
| 12 |
| 7 |
| 12 |
分析：首先把这些分数通分从小到大排列为：
，
，
，
，
，
，
，
，
，它们相加的和为
+
+
+
+
+
+
+
+
=
=
；①使每一横行，每一竖行，两对角线斜行中三个数的和都相等，所以这三个数的和为
=
；②中心数为
；③
+
+
=
+
+
=
+
+
=
+
+
=
；适当调整把原数填入表格解决问题．
| 1 |
| 12 |
| 2 |
| 12 |
| 3 |
| 12 |
| 4 |
| 12 |
| 5 |
| 12 |
| 6 |
| 12 |
| 7 |
| 12 |
| 8 |
| 12 |
| 9 |
| 12 |
| 1 |
| 12 |
| 2 |
| 12 |
| 3 |
| 12 |
| 4 |
| 12 |
| 5 |
| 12 |
| 6 |
| 12 |
| 7 |
| 12 |
| 8 |
| 12 |
| 9 |
| 12 |
| 45 |
| 12 |
| 15 |
| 4 |
| 15 |
| 12 |
| 5 |
| 4 |
| 5 |
| 12 |
| 1 |
| 12 |
| 5 |
| 12 |
| 9 |
| 12 |
| 2 |
| 12 |
| 5 |
| 12 |
| 8 |
| 12 |
| 3 |
| 12 |
| 5 |
| 12 |
| 7 |
| 12 |
| 4 |
| 12 |
| 5 |
| 12 |
| 6 |
| 12 |
| 15 |
| 12 |
解答：解：答案如下表：
．
．点评：事实上任何一个3阶幻方一般按下列步骤完成：首先确定每行、每列以及对角线上三个数的和，再次要确定的是中心数，最后确定四角和其它数．
练习册系列答案
优学名师名题系列答案
相关题目
有一个正方形纸板（如图甲），用它可以盖住日历上的九个日期，并能看到其中一个日期．现在将它放在2004年3月的日历上（如图6乙），则纸板盖住的另外八个日期中最大是
一个各条边分别为5厘米、12厘米、13厘米的直角三角形，将它的短直角边对折到斜边上去与斜边相重合，如图所示．问：图中的阴影部分（即折叠的部分）的面积是多少平方厘米？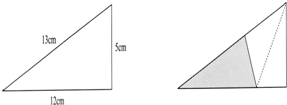
三条边长分别为5厘米、12厘米、13厘米的直角三角形如图．将它的短直角边对折上去与斜边相重合，如右图所示，那么阴影部分（即未被盖住部分）的面积是