题目内容
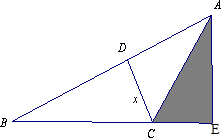
 一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?
一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?分析:根据“将它的短直角边对折到斜边上去与斜边相重合”,可知DC是AB的高,图中阴影部分(即折叠的部分)的面积与△ADC的面积相等;据此只要求出△ADC的底边CD的长,再乘高除以2即可得解;进而根据△ABC的面积=
×AB×DC=
×BC×AE,代入数据即可求出DC的长度,进而得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:见下图:
×13×DC=
×(12-DC)×5,
13×DC=60-DC×5,
DC=
(厘米);
△ADC=△AEC=
×
×5=
(平方厘米).
答:图中的阴影部分(即折叠的部分)的面积是
平方厘米.

| 1 |
| 2 |
| 1 |
| 2 |
13×DC=60-DC×5,
DC=
| 10 |
| 3 |
△ADC=△AEC=
| 1 |
| 2 |
| 10 |
| 3 |
| 25 |
| 3 |
答:图中的阴影部分(即折叠的部分)的面积是
| 25 |
| 3 |
点评:此题考查三角形的面积面积公式的运用,三角形的面积=底×高×
,解决此题关键是先求出DC的长度,进而得解.
| 1 |
| 2 |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
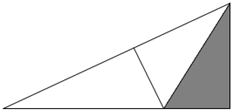 一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?
一个各条边分别为5厘米、12厘米、13厘米的直角三角形,将它的短直角边对折到斜边上去与斜边相重合,如图所示.问:图中的阴影部分(即折叠的部分)的面积是多少平方厘米?