题目内容
10.由一个正方体木块加工成的最大圆柱体,底面周长是18.84厘米,原来正方体木块的体积是216立方厘米:如果再把这个圆柱体加工成最大的圆锥体,这个圆锥的体积是56.52立方厘米.分析 “正方体木块加工成最大的圆柱,底面周长是18.84厘米”,根据圆的周长=πd,即可求出圆的直径,即正方体的棱长,由此利用正方体的体积公式即可解答;
这个最大的圆锥与圆柱等底等高,则圆锥的体积是圆柱的体积的 $\frac{1}{3}$,由此即可解答.
解答 解:18.84÷3.14=6(厘米)
正方体的体积:6×6×6=216(立方厘米)
圆锥的体积:$\frac{1}{3}$×3.14×(6÷2)2×6
=3.14×9×2
=56.52(立方厘米)
答:原来正方体木块的体积是216立方厘米,这个圆锥的体积是56.52立方厘米.
故答案为:216;56.12.
点评 抓住正方体内最大的圆柱的底面直径等于正方体的棱长,再根据正方体和圆锥的体积公式解答即可.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.某地 2006年每月降水量如下表:
(1)根据上表中的数据,完成下面统计图.
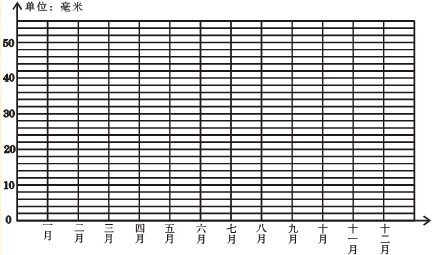
(2)从统计图中,你能获得哪些信息?(写3条信息)①三月降水最多②十二月降水最少③八月降水47毫米.
(3)根据统计图,提出两个问题.①三月比一月降水多多少?②八月比三月降水少多少?.
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 | 十一 | 十二 |
| 降水量 (毫米) | 15 | 23 | 50 | 48 | 32 | 34 | 45 | 47 | 46 | 25 | 18 | 10 |

(2)从统计图中,你能获得哪些信息?(写3条信息)①三月降水最多②十二月降水最少③八月降水47毫米.
(3)根据统计图,提出两个问题.①三月比一月降水多多少?②八月比三月降水少多少?.
19.m×$\frac{1}{8}$=n÷$\frac{1}{5}$( m、n均不为0),那么m( )n.
| A. | > | B. | < | C. | = | D. | 无法确定 |