题目内容
如图．点O是△ABC内一点，且OB平分∠ABC，OC平分∠ACB，∠BOC=130°，则∠A的度数是________．
80°
分析：根据角的平分线的性质和三角形内角和即可解决问题．
解答：根据三角形内角和是180°
∠1+∠3=180°-130°=50°，
OB平分∠ABC，OC平分∠ACB，所以∠ABC+∠ACB=50°×2=100°；
在△ABC中，∠A=180°-100°=80°；
答：∠A的度数是 80°．
故答案为80°．
点评：此题考查了三角形的内角和是180°和角的平分线的性质．要注意转化思想在数学问题中的运用．
分析：根据角的平分线的性质和三角形内角和即可解决问题．
解答：根据三角形内角和是180°
∠1+∠3=180°-130°=50°，
OB平分∠ABC，OC平分∠ACB，所以∠ABC+∠ACB=50°×2=100°；
在△ABC中，∠A=180°-100°=80°；
答：∠A的度数是 80°．
故答案为80°．
点评：此题考查了三角形的内角和是180°和角的平分线的性质．要注意转化思想在数学问题中的运用．
练习册系列答案
阅读快车系列答案
相关题目
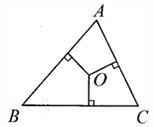如图，三角形ABC的周长是300米，内有一点O，O点到三边的距离都是60米，求三角形ABC的面积．
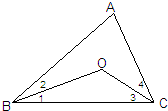如图．点O是△ABC内一点，且OB平分∠ABC，OC平分∠ACB，∠BOC=130°，则∠A的度数是
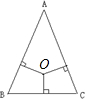如图，三角形ABC中有一点O，O点到三条边的垂线段长都是3厘米．又知道三角形的周长是30厘米，那么三角形ABC的面积是