题目内容
2.用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加上1的规律拼成一列图案(如图):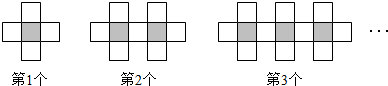
(1)第4个图案中有白色纸片13张,第10个图案中有白色纸片31张.
(2)第a个图案中有白色纸片1+3a张.
分析 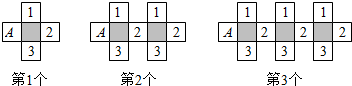
(1)把第1个图案看作:从一个白色A开始增加1次3个白色,一共有:1+3×1个;
(2)把第2个图案看作:从一个白色A开始连续增加2次3个白色,一共有:1+3×2个;
(3)把第3个图案看作:从一个白色A开始连续增加3次3个白色,一共有:1+3×3个;
(4)把第4个图案看作:从一个白色A开始连续增加4次3个白色,一共有:1+3×4个;
(5)同理,把第n个图案看作:从一个白色A开始连续增加n次3个白色,一共有:1+3×n个;
那么根据排列的规律,可得图中有白色纸片个数的公式:1+3n;
由此代入数值,解答即可.
解答 解:(1)根据分析可得图中有白色纸片个数的通项公式:1+3n;
所以第4个图中有白色纸片:1+3×4=13(张);
所以第10个图中有白色纸片:1+3×10=31(张);
答:第4个图案中有白色纸片 13张,第10个图案中有白色纸片 31张.
(2)第a个图案中有白色纸片:1+3a(张).
答:第a个图案中有白色纸片 1+3a张.
故答案为:13,31,1+3a.
点评 此题注意发现:在只考虑白色纸片前后图形中的数量之间的关系的基础上,找到白色纸片的排列的规律即1+3n是本题的解答关键.

练习册系列答案
相关题目
12.公园的一个圆形荷花池直径是30米,它占地( )平方米.
| A. | 9402 | B. | 47.1 | C. | 706.5 |