Question

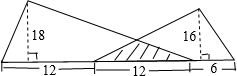（2009?自贡）如图两个三角形部分重叠，重叠部分的面积S占大三角形a的

1

6

，占小三角形面积b的

1

4

，那么a、b的比是（　　），比值是（　　）（单位：cm）

• A．3：2
• B．1.5
• C．2：3
• D．

  2

  3

Answer 1

分析：（1）根据“重叠部分的面积S占大三角形a的

1

6

，”知道大三角形a的面积是S÷

1

6

，再根据“重叠部分的面积S占小三角形面积b的

1

4

，”得出小三角形b的面积是S÷

1

4

，由此即可写出a与b的比，再根据比的基本性质化成最简整数比，即把比的前项和后项同乘一个数或除以一个数（0除外）比值不变；
（2）用比的前项除以后项，即可求出比值．

解答：解：（1）因为a=S÷

1

6

=6S，
b=S÷

1

4

=4S，
所以a：b=6S：4S，
=6：4，
=（6÷2）：（4÷2），
=3：2；
（2）a÷b，
=6S÷4S，
=6÷4，
=

3

2

，
故第一空选：A；第二空选：B；

点评：解答此题的关键是，根据题意写出对应的比，再分别化成最简单的整数比和求比值，注意求比值结果是一个数（整数，小数，分数）；而化简比，结果是一个比．