题目内容
甲乙两人爬山,甲比乙爬得快,各人下山的速度都是各自上山速度的1.5倍,当甲爬到山顶返回后在离山顶60米与乙相遇,当乙爬到山顶时,甲已下到半山腰.求山高多少米?
解:当乙爬到山顶时,甲下到中点,行这条路的 .如果甲继续以上山速度,则只能走这条路的:
.如果甲继续以上山速度,则只能走这条路的: ÷1.5=
÷1.5= ;
;
因此两人速度比为(1+ ):1=4:3,
):1=4:3,
当乙距山顶60米,如果甲不下山继续以上山速度,则只能行60÷1.5=40米,
当乙距离山顶60米时,甲领先乙:60+40=100(米);
100÷( -1)+60
-1)+60
=100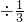 +60,
+60,
=300+60,
=360(米).
答:山高360米.
分析:不让甲下山:
当乙与甲相遇时,甲下山60米.由于各人下山的速度都是各自上山速度的1.5倍,如果甲继续以上山速度,则只能行60÷1.5=40米,也就是当乙距离山顶60米时,甲领先乙:60+40=100(米);当乙爬到山顶时,甲下到中点,行这条路的 .如果甲继续以上山速度,则只能走这条路的:
.如果甲继续以上山速度,则只能走这条路的: ÷1.5=
÷1.5= 可以看到,乙走完山路,则甲走山路的1+
可以看到,乙走完山路,则甲走山路的1+ .
.
因此两人速度比为(1+ ):1=4:3,甲速度为乙的
):1=4:3,甲速度为乙的 .当乙距离山顶150米时,由于用时相等,所以路程和速度成正比例,甲行的路程也是乙的
.当乙距离山顶150米时,由于用时相等,所以路程和速度成正比例,甲行的路程也是乙的 .此时甲多行100米,因此乙行了:100÷(
.此时甲多行100米,因此乙行了:100÷( -1)=300米,此时距离山顶60米,所以山路长为300+60=360米.
-1)=300米,此时距离山顶60米,所以山路长为300+60=360米.
点评:通过让甲不下山继续以上山速度走,根据下山的速度都是各自上山速度的1.5倍求出两人的速度比是完成本题的关键.
 .如果甲继续以上山速度,则只能走这条路的:
.如果甲继续以上山速度,则只能走这条路的: ÷1.5=
÷1.5= ;
;因此两人速度比为(1+
 ):1=4:3,
):1=4:3,当乙距山顶60米,如果甲不下山继续以上山速度,则只能行60÷1.5=40米,
当乙距离山顶60米时,甲领先乙:60+40=100(米);
100÷(
 -1)+60
-1)+60=100
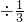 +60,
+60,=300+60,
=360(米).
答:山高360米.
分析:不让甲下山:
当乙与甲相遇时,甲下山60米.由于各人下山的速度都是各自上山速度的1.5倍,如果甲继续以上山速度,则只能行60÷1.5=40米,也就是当乙距离山顶60米时,甲领先乙:60+40=100(米);当乙爬到山顶时,甲下到中点,行这条路的
 .如果甲继续以上山速度,则只能走这条路的:
.如果甲继续以上山速度,则只能走这条路的: ÷1.5=
÷1.5= 可以看到,乙走完山路,则甲走山路的1+
可以看到,乙走完山路,则甲走山路的1+ .
.因此两人速度比为(1+
 ):1=4:3,甲速度为乙的
):1=4:3,甲速度为乙的 .当乙距离山顶150米时,由于用时相等,所以路程和速度成正比例,甲行的路程也是乙的
.当乙距离山顶150米时,由于用时相等,所以路程和速度成正比例,甲行的路程也是乙的 .此时甲多行100米,因此乙行了:100÷(
.此时甲多行100米,因此乙行了:100÷( -1)=300米,此时距离山顶60米,所以山路长为300+60=360米.
-1)=300米,此时距离山顶60米,所以山路长为300+60=360米.点评:通过让甲不下山继续以上山速度走,根据下山的速度都是各自上山速度的1.5倍求出两人的速度比是完成本题的关键.

练习册系列答案
相关题目