题目内容
求阴影部分面积:
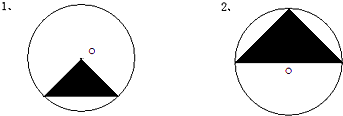
图中两个等腰直角三角形的面积是(1为5平方厘米,2为10平方厘米)求两圆的面积各是多少?
解:(1)假设圆的半径是r,由已知得 r×r=5,
r×r=5,
则r2=10,
圆的面积:πr2=10π(平方厘米);
(2)假设圆的半径是r,根据三角形的面积公式得:
 ×2r×r=10(平方厘米),
×2r×r=10(平方厘米),
则r2=10,
圆的面积:πr2=10π(平方厘米);
答:两圆的面积都是10π平方厘米.
分析:(1)图中阴影部分等腰直角三角形的两个腰垂直且相等,只能是图中圆的半径r,根据三角形的面积公式得 r×r=5平方厘米,则r2=10,然后带入圆的面积公式πr2,即可得解;
r×r=5平方厘米,则r2=10,然后带入圆的面积公式πr2,即可得解;
(2)图中的等腰直角三角形的底边是圆的直径,根据等腰三角形的底边上的高同时是底边上的中线和顶角的角平分线,所以这个三角形的高是圆的半径r,根据三角形的面积公式得 ×2r×r=10平方厘米,得r2=10,然后带入圆的面积公式πr2,即可得解.
×2r×r=10平方厘米,得r2=10,然后带入圆的面积公式πr2,即可得解.
点评:找到等腰直角三角形和圆之间的关系是解决此题的关键.
 r×r=5,
r×r=5,则r2=10,
圆的面积:πr2=10π(平方厘米);
(2)假设圆的半径是r,根据三角形的面积公式得:
 ×2r×r=10(平方厘米),
×2r×r=10(平方厘米),则r2=10,
圆的面积:πr2=10π(平方厘米);
答:两圆的面积都是10π平方厘米.
分析:(1)图中阴影部分等腰直角三角形的两个腰垂直且相等,只能是图中圆的半径r,根据三角形的面积公式得
 r×r=5平方厘米,则r2=10,然后带入圆的面积公式πr2,即可得解;
r×r=5平方厘米,则r2=10,然后带入圆的面积公式πr2,即可得解;(2)图中的等腰直角三角形的底边是圆的直径,根据等腰三角形的底边上的高同时是底边上的中线和顶角的角平分线,所以这个三角形的高是圆的半径r,根据三角形的面积公式得
 ×2r×r=10平方厘米,得r2=10,然后带入圆的面积公式πr2,即可得解.
×2r×r=10平方厘米,得r2=10,然后带入圆的面积公式πr2,即可得解.点评:找到等腰直角三角形和圆之间的关系是解决此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
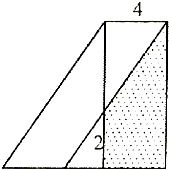 如图中平行四边形的面积是24平方厘米,求阴影部分面积.(单位:厘米)
如图中平行四边形的面积是24平方厘米,求阴影部分面积.(单位:厘米)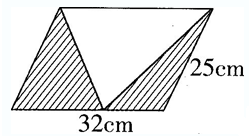 画一画,算一算.
画一画,算一算. 如图求阴影部分面积
如图求阴影部分面积