题目内容
已知一个长方体长、宽、高的和是120厘米,长、宽、高的比是5:4:3,把它截成两个完全一样的长方体,面积最大可增加________平方厘米.
4000
分析:先依据长方体的棱长总和=(长+宽+高)×4,求出长宽高的和,再利用按比例分配的方法分别求出长宽高的值,又因切成小长方体后增加了两个面,要求表面积最多增加多少,则增加的两个面是原长方体的两个最大面,从而问题得解.
解答:120÷4=30(厘米),
120×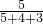 =50(厘米),
=50(厘米),
120× =40(厘米),
=40(厘米),
120-50-40=30(厘米),
50×40×2=4000(平方厘米);
答:面积最大可增加4000平方厘米.
故答案为:4000.
点评:解答此题的关键是明白,切成小长方体后增加了两个面,要求表面积最多增加多少,则增加的两个面是原长方体的两个最大面.
分析:先依据长方体的棱长总和=(长+宽+高)×4,求出长宽高的和,再利用按比例分配的方法分别求出长宽高的值,又因切成小长方体后增加了两个面,要求表面积最多增加多少,则增加的两个面是原长方体的两个最大面,从而问题得解.
解答:120÷4=30(厘米),
120×
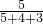 =50(厘米),
=50(厘米),120×
 =40(厘米),
=40(厘米),120-50-40=30(厘米),
50×40×2=4000(平方厘米);
答:面积最大可增加4000平方厘米.
故答案为:4000.
点评:解答此题的关键是明白,切成小长方体后增加了两个面,要求表面积最多增加多少,则增加的两个面是原长方体的两个最大面.

练习册系列答案
相关题目