题目内容
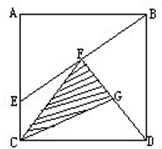 如图,ABCD是长方形,其中 AB=8,AE=6,EC=3.并且F是线段BE的中点,G是线段FD的中点.求三角形CFG(阴影部分)的面积.
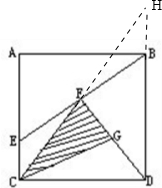
如图,ABCD是长方形,其中 AB=8,AE=6,EC=3.并且F是线段BE的中点,G是线段FD的中点.求三角形CFG(阴影部分)的面积.分析:延长CF,交DB的延长线于点H,不难发现三角形CEF与三角形HBF是全等三角形,则EC=HB,CF=HF,由此可得:DH=6+3+3=12,F是CH的中点,根据高一定时,三角形的面积与底成正比例的性质可得:三角形CDF的面积=
三角形CDH的面积=
×(6+3+3)×8÷2=24,因为G是ED的中点,所以阴影部分的面积=
×24=12.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

解答:解:延长CF,交DB的延长线于点H,不难发现三角形CEF与三角形HBF是全等三角形,则EC=HB,CF=HF,
由此可得:DH=6+3+3=12,F是CH的中点,
又因为CD=AB=8,
所以三角形CDF的面积=
×三角形CDH的面积=
×12×8÷2=24,
因为G是ED的中点,所以阴影部分的面积=
×三角形CDF的面积=
×24=12.
答:阴影部分的面积是12.
由此可得:DH=6+3+3=12,F是CH的中点,
又因为CD=AB=8,
所以三角形CDF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
因为G是ED的中点,所以阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
答:阴影部分的面积是12.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用,解答此题的关键是利用辅助线进行等积变形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
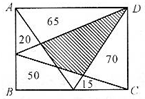 如图,ABCD是长方形,图中的数是各部分的面积数,则图中阴影部分的面积为
如图,ABCD是长方形,图中的数是各部分的面积数,则图中阴影部分的面积为 如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是
如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是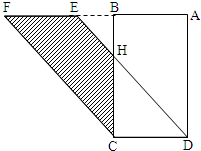 如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积.
如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积. 如图,ABCD是长方形,AB=10cm,BC=6cm,AC、BD交于点O,图中阴影部分以CD为轴旋转一周.则阴影部分扫过的立体图形的体积是多少立方厘米?
如图,ABCD是长方形,AB=10cm,BC=6cm,AC、BD交于点O,图中阴影部分以CD为轴旋转一周.则阴影部分扫过的立体图形的体积是多少立方厘米?