题目内容
 如图,把正方形ACFG与Rt△ACB按如图①所示重叠在一起,其中AC=2,∠BAC=60°,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得△A′B′C,AB分别与A′C、A′B′相交于点D、E,如图②所示
如图,把正方形ACFG与Rt△ACB按如图①所示重叠在一起,其中AC=2,∠BAC=60°,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得△A′B′C,AB分别与A′C、A′B′相交于点D、E,如图②所示(1)△ABC至少旋转多少度才能得到△A'B'C?说明理由;
(2)求△ABC与△A′B′C重叠部分(即四边形CDEF)的面积.
分析:(1)根据题意,结合旋转的性质:可得△A′CF是等边三角形,进而可得∠ACA′=90°-60°=30°,故至少应旋转30°;
(2)根据题意分别求得△A′DE的面积与△ABC的面积;观察图形分析可得四边形DCFE的面积为:S△A’CF-S△A′DE,代入数据可得答案.
(2)根据题意分别求得△A′DE的面积与△ABC的面积;观察图形分析可得四边形DCFE的面积为:S△A’CF-S△A′DE,代入数据可得答案.
解答:解:(1)因为ACFG是正方形,A'B′经过点F,
所以A′C=CF.
又因为∠A′=60°,
所以△A′CF是等边三角形.
因为∠A′CF=60°,
所以∠ACA′=90°-60°=30°.
所以△ABC至少旋转30°才能得到△A′CB′.
(2)因为∠ACA′=30°,∠BAC=60°,
所以∠A′DE=90°.
又因为AC=2,
可求得CD=
,A′D=2-
.
在Rt△A′DE中,
DE=A′Dtan60°=(2-
)?
=2
-3.
所以△A′DE的面积为:
A′D?DE=(2-
)?(2
-3)=
-6.
又因为A'B′=4,A′F=2,
所以F是A'B′的中点.
所以△A′CF的面积=
△ABC的面积.
而B′C=A′C?tan60°=2
,
S△ABC=
×2×2
=2
,S△A’CF=
,
所以四边形CDEF的面积为:
-(
-6)=
-
+6=6-
;
(若取近似值,则结果应约为1.7.).
所以A′C=CF.
又因为∠A′=60°,
所以△A′CF是等边三角形.
因为∠A′CF=60°,
所以∠ACA′=90°-60°=30°.
所以△ABC至少旋转30°才能得到△A′CB′.
(2)因为∠ACA′=30°,∠BAC=60°,
所以∠A′DE=90°.
又因为AC=2,
可求得CD=
| 3 |
| 3 |
在Rt△A′DE中,
DE=A′Dtan60°=(2-
| 3 |
| 3 |
| 3 |
所以△A′DE的面积为:
| 1 |
| 2 |
| 3 |
| 3 |
| 7 |
| 2 |
| 3 |
又因为A'B′=4,A′F=2,
所以F是A'B′的中点.
所以△A′CF的面积=
| 1 |
| 2 |
而B′C=A′C?tan60°=2
| 3 |
S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
所以四边形CDEF的面积为:
| 3 |
| 7 |
| 2 |
| 3 |
| 3 |
| 7 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
(若取近似值,则结果应约为1.7.).
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
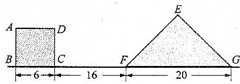 如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?
如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?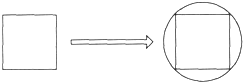 如图,把正方形桌面的四边撑开后,就成了一张圆桌面,圆桌面的面积为π平方米,那么,正方形桌面的面积是( )平方米.
如图,把正方形桌面的四边撑开后,就成了一张圆桌面,圆桌面的面积为π平方米,那么,正方形桌面的面积是( )平方米.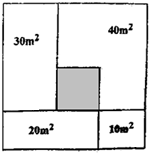 如图,把正方形的土地分成如下四个长方形(它们的面积分别为10平方米、20平方米、30平方米、40平方米),阴影部分是正方形且它包含在40平方米的长方形之内.求阴影部分的面积.
如图,把正方形的土地分成如下四个长方形(它们的面积分别为10平方米、20平方米、30平方米、40平方米),阴影部分是正方形且它包含在40平方米的长方形之内.求阴影部分的面积.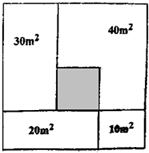 如图,把正方形的土地分成如下四个长方形(它们的面积分别为10平方米、20平方米、30平方米、40平方米),阴影部分是正方形且它包含在40平方米的长方形之内.求阴影部分的面积.
如图,把正方形的土地分成如下四个长方形(它们的面积分别为10平方米、20平方米、30平方米、40平方米),阴影部分是正方形且它包含在40平方米的长方形之内.求阴影部分的面积.