题目内容
 如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB、BC、CD滚到2的位置,如果AB、BC、CD的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?
如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB、BC、CD滚到2的位置,如果AB、BC、CD的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?分析:圆板的正面滚过的部分如图阴影部分所求,它的面积列式为:
结合图计算即可.
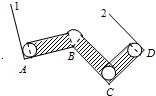
| 三个长方形的面积=(20-2)×4+(20-4)×4+(20-6)×4=192,最开始和结束时的两个半圆的面积=π×22=4π, B点处滚动的扇形的面积=π×42×1/6=8/3π,C点处滚动的扇形的面积=2×2×3+π×22×1/4=12+π, 面积=192+4π+8/3π+12+π=204+23/3π≈228.07; |

解答: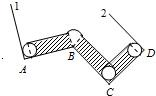 解:
解:
×π×22+(20-2)×4+
×π×42-
×(42-π×22)+
×π×22
=204+
π
≈228.07(平方厘米).
答:圆板的正面滚过的面积约是228.07平方厘米.
 解:
解:| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
=204+
| 23 |
| 3 |
≈228.07(平方厘米).
答:圆板的正面滚过的面积约是228.07平方厘米.
点评:考查了滚动图形的面积计算,本题需要分段进行计算,再将各段相加求解.

练习册系列答案
相关题目
 一个底面半径为2.5分米的圆柱形玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少?
一个底面半径为2.5分米的圆柱形玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少? 如图所示,把一块半径为10厘米的圆形铁片,去掉
如图所示,把一块半径为10厘米的圆形铁片,去掉 一个底面半径为2.5分米的圆柱形玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少?
一个底面半径为2.5分米的圆柱形玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少? 如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB、BC、CD滚到2的位置,如果AB、BC、CD的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?
如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB、BC、CD滚到2的位置,如果AB、BC、CD的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?