Question

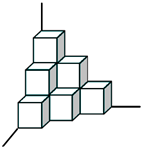如图，靠墙的角落将若干个小正方体搭成一个立体图形，这些小正方体的个数有

 

个，露在外面的面有

 

个面．如果每个小正方体的棱长是2厘米，那么露在外面的面的面积是

 

平方厘米．这个立体图形的体积是

 

立方厘米．

Answer 1

分析：该立方体共3层，从上向下数：一层有1个，二层有3个，三层有6个，共有1+3+6=10个小正方体，露在外面的面一共有：从上面看有6个，从前面看有6个，从右面看有6个，一共有6×3=18个，由此利用正方形的面积公式求出每个小正方体的面的面积，再乘18就是露在外部的总面积；根据正方体的体积公式求出每个小正方体的体积，再乘正方体的总个数就是这个立体图形的体积．

解答：解：（1）图中几何体露出的面有：6×3=18（个），
所以这个几何体的表面积是：2×2×18=72（平方厘米）；

（2）这个几何体共有3层组成，
所以共有小正方体的个数为：1+3+6=10（个），
所以这个几何体的体积为：2×2×2×10=80（立方厘米）；
答：这个图形的表面积是72平方厘米，体积是80立方厘米．
故答案为：10，18，72，80．

点评：此题考查了观察几何体的方法的灵活应用；抓住这个几何体的体积等于这些小正方体的体积之和；几何体的表面积是露出的小正方体的面的面积之和是解决此类问题的关键．