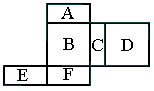
题目内容
如图,下列几何体都是由若干个边长为1的小正方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第2008个几何体中只有两个面涂色的小正方体共有
16060
16060
个.
分析:根据所给图形中只有2个面涂色的小立方体的块数得到第n个几何体中只有2个面涂色的小立方体的块数与4的倍数的关系,然后进行解答即可;
解答:解:(1)观察图形可知:图①中,两面涂色的小立方体共有4个;
图②中,两面涂色的小立方体共有12个;
图③中,两面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n-1)=8n-4,
当第2008个几何体中只有两面涂色的小立方体有:
2008×8-4,
=16060(个);
故答案为:16060.
图②中,两面涂色的小立方体共有12个;
图③中,两面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n-1)=8n-4,
当第2008个几何体中只有两面涂色的小立方体有:
2008×8-4,
=16060(个);
故答案为:16060.
点评:考查图形的变化规律;得到所求块数与4的倍数的关系是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目