题目内容
一个边长为acm的正方形（a＞2），相邻的两个边中，一个边增加2cm，一个边减少2cm，那么（ ）
分析：由题意可知：一个边增加2厘米，另一个边减少2厘米，则图形的周长就等于原正方形的周长；然后分别求出改变前后各图形的边长，从而得出面积，即可知道面积的变化情况．
解答：解：设原正方形的边长为a，则变化后的图形的长为（a+2），宽为（a-2），
原正方形的周长：a×4=4a（厘米），
新长方形的周长：（a+2+a-2）×2=4a（厘米）；
正方形的面积：a×a=a2（平方厘米），
长方形的面积：（a+2）×（a-2）=a2-4（平方厘米）；
所以：周长不变，面积减少4平方厘米．
故答案为：B．
原正方形的周长：a×4=4a（厘米），
新长方形的周长：（a+2+a-2）×2=4a（厘米）；
正方形的面积：a×a=a2（平方厘米），
长方形的面积：（a+2）×（a-2）=a2-4（平方厘米）；
所以：周长不变，面积减少4平方厘米．
故答案为：B．
点评：解答此题的关键是：分别求出变化后的图形的边长，利用正方形和长方形的周长和面积公式，即可比较出周长和面积的变化．
练习册系列答案
全能练考卷系列答案
相关题目
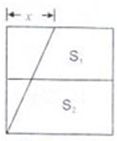一个边长为10cm的正方形被两条线段分割成两个等高的直角梯形S1、S2和一个直角三角形．已知S1、S2的面积相差10cm2，那么图中x的值是