Question

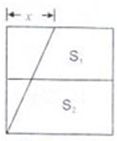一个边长为10cm的正方形被两条线段分割成两个等高的直角梯形S₁、S₂和一个直角三角形．已知S₁、S₂的面积相差10cm²，那么图中x的值是

4

cm．

Answer 1

分析：根据题干，这两个梯形的高相等都是10÷2=5厘米，设两个等高的直角梯形S₁、S₂的公共底边为a，则根据梯形的面积公式即可用含有a和x的式子表示出S₁、S₂，再根据两个梯形的面积之差是10平方厘米，列出方程解决问题．

解答：解：设公共底边为a，根据题意可得方程：
（a+10）×（10÷2）÷2-（10-x+a）×（10÷2）÷2=10
                         2.5a+25-25+2.5x-2.5a=10
                                         2.5x=10
                                            x=4
答：图中x的值是4厘米．
故答案为：4．

点评：解答此题的关键是明确梯形的上下底与高的值，利用梯形的面积公式表示出两个图形的面积，再根据面积之差是10平方厘米列出方程解决问题．