题目内容
 选做题.
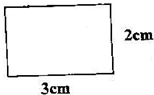
选做题.如图中的长方形绕它的长或宽旋转一周,可分别得到立标图形A和B.
(1)算一算立体图形A、B的体积.
(2)立体图形A和B的体积之比与原长方形有何关系?(请用数学式子或文字加以说明)
分析:(1)将长方形绕长旋转一周,得到一个圆柱体A,圆柱体的高是3厘米,底面半径是2厘米;绕宽旋转一周得到一个圆柱体B,圆柱体的高是2厘米,底面半径是3厘米,根据圆柱的体积=πr2h计算即可解答;
(2)求出两个圆柱的体积比,与原长方形比较即可得出结论.
(2)求出两个圆柱的体积比,与原长方形比较即可得出结论.
解答:解:(1)A的体积为:3.14×3×22=37.68(立方厘米);
B的体积为:3.14×32×2=56.52(立方厘米);
答:立体图形A的体积是37.68立方厘米,B的体积是56.52立方厘米.
(2)立体图形A和B的体积之比是:
(3.14×3×22):(3.14×32×2)=2:3;
原长方形的宽与长的比是2:3;
所以立体图形A和B的体积之比等于原长方形宽与长的长度之比.
答:立体图形A和B的体积之比等于原长方形宽与长的长度之比.
B的体积为:3.14×32×2=56.52(立方厘米);
答:立体图形A的体积是37.68立方厘米,B的体积是56.52立方厘米.
(2)立体图形A和B的体积之比是:
(3.14×3×22):(3.14×32×2)=2:3;
原长方形的宽与长的比是2:3;
所以立体图形A和B的体积之比等于原长方形宽与长的长度之比.
答:立体图形A和B的体积之比等于原长方形宽与长的长度之比.
点评:解决本题的关键是得出旋转后图形的底面半径和高.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
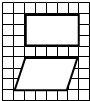 (2008?长汀县)如图中的长方形和平行四边形比较,( )
(2008?长汀县)如图中的长方形和平行四边形比较,( )