题目内容
在括号内填上两个不同的正整数,使等式
=
+
成立.同样,找出两个不同的正整数,使等式
=
+
,
=
+
成立.
| 1 |
| 2 |
| 1 |
| ( ) |
| 1 |
| ( ) |
| 1 |
| 5 |
| 1 |
| ( ) |
| 1 |
| ( ) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| ( ) |
分析:可以从最简单的入手,先填入3试一试即
=
+
,进而可得
=
-
=
,所以
=
+
;
同理:
-
=
,可得
=
+
;
-
=
,可得
=
+
;
-
=
,可得
=
+
;…
根据分母之间的关系可得出规律:
=
+
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| ( ) |
| 1 |
| ( ) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
同理:
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 30 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 30 |
根据分母之间的关系可得出规律:
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n×(n+1) |
解答:解:(1)
=
+
;
(2)
=
+
;
(3)
=
+
;
故答案为:3、6;6、30;n×(n+1).
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(2)
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 30 |
(3)
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n×(n+1) |
故答案为:3、6;6、30;n×(n+1).
点评:“式”的规律题,研究时可以从最简单的入手,经过尝试调整就可找出规律.本题的关键是:尝试填入数后,得出的差的分母是否为1.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
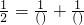 成立.同样,找出两个不同的正整数,使等式
成立.同样,找出两个不同的正整数,使等式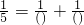 ,
,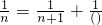 成立.
成立.