题目内容
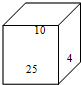有一个正方体木块（如图），每个面各写了一个自然数，并且相对的两个面上的两个数之和相等．现在只能看见三个面上写的数，如果看不见的各面写的都是质数，那么这三个质数的和是分析：设25对面的数为a，10对面的数为b，4对面的数为c，依题意列出等式，再根据数的奇偶性进行分析．
解答：解：设25对面的数为a，10对面的数为b，4对面的数为c，
依题意，得25+a=10+b=4+c，
因为a、b、c为质数，最小的质数为2，
所以b、c为奇数，
所以25+a，10+b，4+c都为奇数，
由25+a为奇数，a为质数可知，a=2，
由此可得10+b=4+c=27，
解得b=17，c=23，
则这三个质数的和是：2+17+23=42；
答：这三个质数的和是42；
故答案为：42．
依题意，得25+a=10+b=4+c，
因为a、b、c为质数，最小的质数为2，
所以b、c为奇数，
所以25+a，10+b，4+c都为奇数，
由25+a为奇数，a为质数可知，a=2，
由此可得10+b=4+c=27，
解得b=17，c=23，
则这三个质数的和是：2+17+23=42；
答：这三个质数的和是42；
故答案为：42．
点评：本题考查了奇数与偶数．关键是根据题意列出等式，根据相等的数奇偶性相同解题．
练习册系列答案
相关题目
有一个正方体木块，木块六个面上分别写着数字1、2、3、4、5、6．其中，1与4，2与5，3与6相对．现在把这个木块放在如图第一格内（看得见的三个面上的数字如图所示，其中朝上的面上写着数字1）．如果将木块沿着图中的方格滚动（每次滚动一小格），当木块滚到第22个格时，木块朝上的面上写着的数字是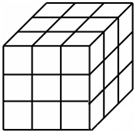
有一个正方体木块，外表全部涂上红色后将它切成27个小正方体（如图），切好后：
把一个正方体木块的表面全涂成红色，然后切成27个小正方体（如图），那么，三面涂色的有