题目内容
 把一个正方体木块的表面全涂成红色,然后切成27个小正方体(如图),那么,三面涂色的有
把一个正方体木块的表面全涂成红色,然后切成27个小正方体(如图),那么,三面涂色的有8
8
个,二个面是红色的小正方体有12
12
个.一个面是红色的小正方体有6
6
个,没有涂色的小正方体有1
1
个.分析:根据正方体表面涂色的特点,分别得出切割后的小正方体涂色面的排列特点:(1)三面涂色的在每个顶点处;(2)两面涂色的在每条棱长上(除去顶点处的小正方体);(3)一面涂色的都在每个面上(除去棱长上的小正方体);(4)没有涂色的都在内部.
解答:解:(1)三面涂色的在每个顶点处,共有8个;
(2)两面涂色的在每条棱长上(除去顶点处的小正方体),有(3-2)×12=12(个);
(3)一面涂色的都在每个面上(除去棱长上的小正方体),有1×6=6(个);
(4)没有涂色的都在内部,27-8-12-6=1(个).
故答案为:8,12,6,1.
(2)两面涂色的在每条棱长上(除去顶点处的小正方体),有(3-2)×12=12(个);
(3)一面涂色的都在每个面上(除去棱长上的小正方体),有1×6=6(个);
(4)没有涂色的都在内部,27-8-12-6=1(个).
故答案为:8,12,6,1.
点评:解决此类问题的关键是抓住:三面涂色的在顶点处;两面涂色的在每条棱长的中间上;一面涂色的每个在面的中心上;没有涂色的在内部.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图是一个正方体木块的表面展开图,如果在正方体的各个面上填上数,使得对面两数之和都是7,那么A是
如图是一个正方体木块的表面展开图,如果在正方体的各个面上填上数,使得对面两数之和都是7,那么A是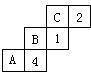 如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?
如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?