题目内容
如图,大、小两个正方形拼在一起,比较图中两块阴影部分面积的大小:
S△ABE

S△ABE
=
=
S△CDE.分析:如图所示,三角形CDA和三角形BDA等底等高,则它们的面积相等,分别去掉公共部分(三角形AED),则剩余部分的面积相等,即三角形ABE和三角形CDE的面积相等;据此解答.
解答:解:如图: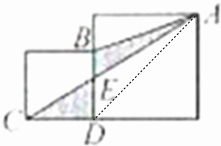
连接AD,则可以得出:
三角形CDA和三角形BDA等底等高,则它们的面积相等,分别去掉公共部分(三角形AED),则剩余部分的面积相等,即三角形ABE和三角形CDE的面积相等;
故答案为:=.

连接AD,则可以得出:
三角形CDA和三角形BDA等底等高,则它们的面积相等,分别去掉公共部分(三角形AED),则剩余部分的面积相等,即三角形ABE和三角形CDE的面积相等;
故答案为:=.
点评:由题意推出:三角形CDA和三角形BDA等底等高,则它们的面积相等,是解答本题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
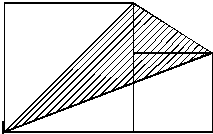 如图:大、小两个正方形连在一起,且大正方形边长为15,求阴影面积.
如图:大、小两个正方形连在一起,且大正方形边长为15,求阴影面积. 有一个圆柱体,高是底面半径的3倍.将它如图分成大、小两个圆柱体,大圆柱体的表面积是小圆柱体的3倍.那么,大圆柱体的体积是小圆柱体的
有一个圆柱体,高是底面半径的3倍.将它如图分成大、小两个圆柱体,大圆柱体的表面积是小圆柱体的3倍.那么,大圆柱体的体积是小圆柱体的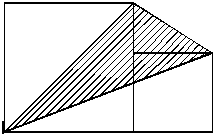 如图:大、小两个正方形连在一起,且大正方形边长为15,求阴影面积.
如图:大、小两个正方形连在一起,且大正方形边长为15,求阴影面积.