19.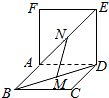 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.以下命题中真命题的序号是( )
①若棱柱被一平面所截,则分成的两部分不一定是棱柱;
②有两个面平行,其余各面都是梯形的几何体叫棱台;
③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;
④有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
①若棱柱被一平面所截,则分成的两部分不一定是棱柱;
②有两个面平行,其余各面都是梯形的几何体叫棱台;
③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;
④有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
| A. | ③④ | B. | ①④ | C. | ①②④ | D. | ① |
15.已知三棱柱ABC-A1B1C1的侧棱长为4,底面边长都为3,A1在底面ABC上的射影为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{3}}{16}$ | D. | $\frac{3}{16}$ |
14.设函数y=sinx在区间$[t,t+\frac{π}{2}]$上的最大值为M(t),最小值为m(t),则M(t)-m(t)的最小值和最大值分别为( )
0 252843 252851 252857 252861 252867 252869 252873 252879 252881 252887 252893 252897 252899 252903 252909 252911 252917 252921 252923 252927 252929 252933 252935 252937 252938 252939 252941 252942 252943 252945 252947 252951 252953 252957 252959 252963 252969 252971 252977 252981 252983 252987 252993 252999 253001 253007 253011 253013 253019 253023 253029 253037 266669
| A. | 1,2 | B. | $1,\sqrt{2}$ | C. | $1-\frac{{\sqrt{2}}}{2},1$ | D. | $1-\frac{{\sqrt{2}}}{2},\sqrt{2}$ |