53.[山东省潍坊市2007-2008学年度高三第一学期期末考试数学试题文科第16题,理科第15题]
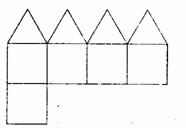 已知一个凸多面体共有9个面,所有棱长均为1,
已知一个凸多面体共有9个面,所有棱长均为1,
其平面展开图如右图所示,则该凸多面体的体积
V= ;
53.[山东省潍坊市2007-2008学年度高三第一学期期末考试数学试题文科第16题,理科第15题]
 已知一个凸多面体共有9个面,所有棱长均为1,
已知一个凸多面体共有9个面,所有棱长均为1,
其平面展开图如右图所示,则该凸多面体的体积
V= ;