摘要:又由函数是减函数.得
网址:http://m.1010jiajiao.com/timu_id_95411[举报]
已知函数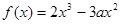 ,
, ,又函数
,又函数 在
在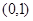 单调递减,而在
单调递减,而在 单调递增.
单调递增.
(1)求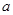 的值;
的值;
(2)求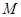 的最小值,使对
的最小值,使对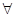
 ,有
,有 成立;
成立;
(3)是否存在正实数 ,使得
,使得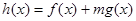 在
在 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
已知函数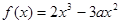 ,
,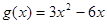 ,又函数
,又函数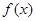 在
在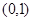 单调递减,而在
单调递减,而在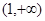 单调递增.
单调递增.
(1)求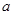 的值;
的值;
(2)求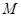 的最小值,使对
的最小值,使对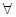
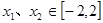 ,有
,有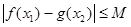 成立;
成立;
(3)是否存在正实数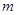 ,使得
,使得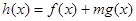 在
在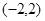 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
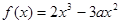 ,
,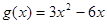 ,又函数
,又函数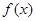 在
在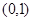 单调递减,而在
单调递减,而在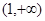 单调递增.
单调递增.(1)求
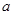 的值;
的值;(2)求
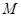 的最小值,使对
的最小值,使对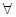
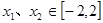 ,有
,有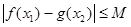 成立;
成立;(3)是否存在正实数
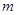 ,使得
,使得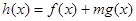 在
在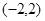 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
已知函数f(x)=2x3-3ax2,g(x)=3x2-6x,又函数f(x)在(0,1)单调递减,而在(1,+∞)单调递增.
(1)求a的值;
(2)求M的最小值,使对?x1、x2∈[-2,2],有|f(x1)-g(x2)|≤M成立;
(3)是否存在正实数m,使得h(x)=f(x)+mg(x)在(-2,2)上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由. 查看习题详情和答案>>
(1)求a的值;
(2)求M的最小值,使对?x1、x2∈[-2,2],有|f(x1)-g(x2)|≤M成立;
(3)是否存在正实数m,使得h(x)=f(x)+mg(x)在(-2,2)上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由. 查看习题详情和答案>>