摘要:(I)在使得..有意义的条件下.试比较的大小,
网址:http://m.1010jiajiao.com/timu_id_93363[举报]
设![]() ,
,![]() ,Q=
,Q=![]() ;若将
;若将![]() ,
,![]() ,
,![]() 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列![]() 的前三项
的前三项
![]() (I)在使得
(I)在使得![]() ,
,![]() ,
,![]() 有意义的条件下,试比较
有意义的条件下,试比较![]() 的大小;
的大小;
(II)求![]() 的值及数列
的值及数列![]() 的通项;
的通项;
(III)记函数![]() 的图象在
的图象在![]() 轴上截得的线段长为
轴上截得的线段长为![]() ,设
,设![]() ,求
,求![]() .
.
设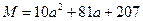 ,
,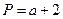 ,Q=
,Q=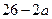 ;若将
;若将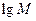 ,
,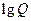 ,
,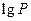 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列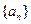 的前三项
的前三项
 (I)在使得
(I)在使得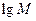 ,
,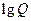 ,
,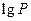 有意义的条件下,试比较
有意义的条件下,试比较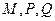 的大小;
的大小;
(II)求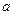 的值及数列
的值及数列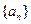 的通项;
的通项;
(III)记函数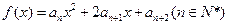 的图象在
的图象在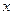 轴上截得的线段长为
轴上截得的线段长为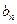 ,设
,设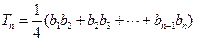 ,求
,求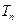 .
.
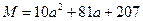 ,
,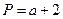 ,Q=
,Q=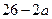 ;若将
;若将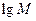 ,
,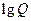 ,
,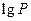 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列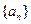 的前三项
的前三项 (I)在使得
(I)在使得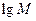 ,
,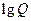 ,
,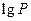 有意义的条件下,试比较
有意义的条件下,试比较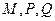 的大小;
的大小;(II)求
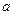 的值及数列
的值及数列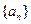 的通项;
的通项;(III)记函数
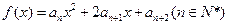 的图象在
的图象在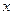 轴上截得的线段长为
轴上截得的线段长为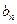 ,设
,设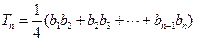 ,求
,求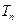 .
.
设M是由满足下列条件的函数f(x)构成的集合:“①方程f(x)-x=0有实数根;②函数f(x)的导数f′(x)满足
0<f′(x)<1”
(I)证明:函数f(x)=
+
(0≤x<
)是集合M中的元素;
(II)证明:函数f(x)=
+
(0≤x<
)具有下面的性质:对于任意[m,n]⊆[0,
),都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.
(III)若集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意[m,n]⊆D,都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.试用这一性质证明:对集合M中的任一元素f(x),方程f(x)-x=0只有一个实数根. 查看习题详情和答案>>
0<f′(x)<1”
(I)证明:函数f(x)=
| 3x |
| 4 |
| x3 |
| 3 |
| 1 |
| 2 |
(II)证明:函数f(x)=
| 3x |
| 4 |
| x3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(III)若集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意[m,n]⊆D,都存在xo∈(m,n),使得等式f(n)-f(m)=(n-m)f′(xo)成立.试用这一性质证明:对集合M中的任一元素f(x),方程f(x)-x=0只有一个实数根. 查看习题详情和答案>>