摘要：即对一切的正整数恒成立.．
网址：http://m.1010jiajiao.com/timu_id_92564[举报]
设不等式组
所表示的平面区域为Dn，记Dn内的整点个数为an（n∈N*）（整点即横坐标与纵坐标均为整数的点）．
（1）求数列{an}的通项公式；
（2）（理）设Sn=
+
+…+
，求Sn的最小值（n＞1，n∈N*）；
（3）设Tk=
+
+…+
求证：T2n≥
(n＞1，n∈N*)．
（文）记数列{an}的前n项和为Sn，且Tn=
．若对一切的正整数n，总有Tn≤m，求实数m的取值范围．
查看习题详情和答案>>
|
（1）求数列{an}的通项公式；
（2）（理）设Sn=
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
（3）设Tk=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| ak |
| 7n+11 |
| 36 |
（文）记数列{an}的前n项和为Sn，且Tn=
| Sn |
| 3•2n-1 |
不等式组
所表示的平面区域为Dn，若Dn内的整点（整点即横坐标和纵坐标均为整数的点）个数为an（n∈N*）
（1）写出an+1与an的关系（只需给出结果，不需要过程），
（2）求数列{an}的通项公式；
（3）设数列an的前n项和为Sn且Tn=
，若对一切的正整数n，总有Tn≤m成立，求m的范围．
查看习题详情和答案>>
|
（1）写出an+1与an的关系（只需给出结果，不需要过程），
（2）求数列{an}的通项公式；
（3）设数列an的前n项和为Sn且Tn=
| Sn |
| 5•2n |
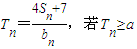对一切的正整数n恒成立，则a的取值范围为（ ）
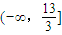
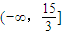
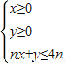所表示的平面区域为Dn，若Dn内的整点（整点即横坐标和纵坐标均为整数的点）个数为an（n∈N*）
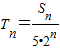，若对一切的正整数n，总有Tn≤m成立，求m的范围．