摘要:(Ⅲ)若函数的最大值为8.求的值.
网址:http://m.1010jiajiao.com/timu_id_92484[举报]
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴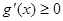 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
查看习题详情和答案>>
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
.
(1)求φ;
(2)若函数y=2f(x)+a,(a为常数a∈R)在x∈[
,
]上的最大值和最小值之和为1,求a的值.
查看习题详情和答案>>
| π |
| 8 |
(1)求φ;
(2)若函数y=2f(x)+a,(a为常数a∈R)在x∈[
| 11π |
| 24 |
| 3π |
| 4 |
设函数f(x)=2sin2(ωx+
)+2cos2ωx(ω>0)的图象上两个相邻的最低点之间的距离为
(1)求函数f(x)的最大值,并求出此时x的值;
(2)若函数g(x)的图象是由f(x)的图象向右平移
个单位长度,再沿y轴对称后得到的,求函数g(x)的单调减区间.
查看习题详情和答案>>
| π |
| 4 |
| 2π |
| 3 |
(1)求函数f(x)的最大值,并求出此时x的值;
(2)若函数g(x)的图象是由f(x)的图象向右平移
| π |
| 8 |