摘要:知.MN的方程为cx+by+c2=(a-c)2,由已知-=-1.
网址:http://m.1010jiajiao.com/timu_id_91340[举报]
已知幂函数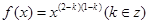 满足
满足 。
。
(1)求实数k的值,并写出相应的函数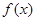 的解析式;
的解析式;
(2)对于(1)中的函数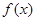 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数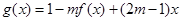 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数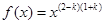 满足
满足 ,得到
,得到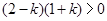
因为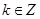 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,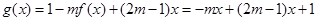 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: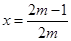 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到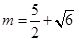
(1)对于幂函数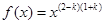 满足
满足 ,
,
因此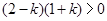 ,解得
,解得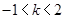 ,………………3分
,………………3分
因为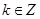 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数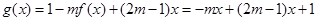 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: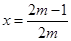 ,
,
当 时,
时,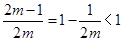 ,因为在区间
,因为在区间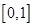 上的最大值为5,
上的最大值为5,
所以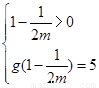 ,或
,或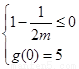 …………………………………………10分
…………………………………………10分
解得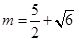 满足题意
满足题意
查看习题详情和答案>>
已知点A(-1,0),B(1,0),直线AM,BM相交于点M,且kMA×kMB=-2.
(1)求点M的轨迹C的方程;
(2)过定点(0,1)作直线PQ与曲线C交于P,Q两点,且|PQ|=
,求直线PQ的方程.
查看习题详情和答案>>
(1)求点M的轨迹C的方程;
(2)过定点(0,1)作直线PQ与曲线C交于P,Q两点,且|PQ|=
3
| ||
| 2 |
已知函数f(x)=
(m>1),且满足f(x+4)=f(x).若函数F(x)=f(x)-x恰好有3个零点,则实数m的取值范围为( )
|
A、(4,2
| ||||
B、(
| ||||
| C、(4,8) | ||||
D、[
|
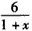 ∈Z},求M;
∈Z},求M;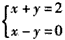 的解集;
的解集;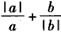 (a,b∈R)所确定的实数集合.
(a,b∈R)所确定的实数集合.