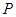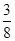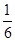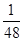网址:http://m.1010jiajiao.com/timu_id_88710[举报]
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为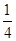 ,不堵车的概率为
,不堵车的概率为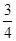 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为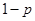 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为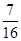 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得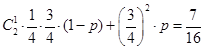
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 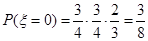 ,
, 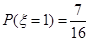
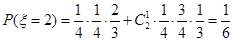 ,
,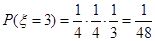
从而得到分布列和期望值
解:(I)由已知条件得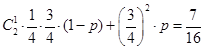 ,即
,即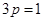 ,则
,则 的值为
的值为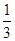 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 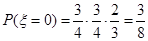 ,
, 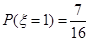
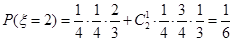 ,
,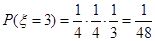
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以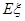
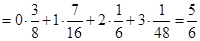
查看习题详情和答案>>
某市投资甲、乙两个工厂,2011年两工厂的产量均为100万吨,在今后的若干年内,甲工厂的年产量每年比上一年增加10万吨,乙工厂第 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 年的年产量分别为
年的年产量分别为 万吨和
万吨和 万吨.
万吨.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若某工厂年产量超过另一工厂年产量的2倍,则将另一工厂兼并,问到哪一年底,其中哪一个工厂被另一个工厂兼并.
【解析】本试题主要考查数列的通项公式的运用。
第一问由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二问,考查等差数列与等比数列的综合,考查用数列解决实际问题,其步骤是建立数列模型,进行计算得出结果,再反馈到实际中去解决问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.
解:(Ⅰ)由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的产量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工厂将被乙工厂兼并
查看习题详情和答案>>
某学校为溺调查了解学生体能状况,决定对高三学生进行一次体育达标测试,具体测试项目有100米跑、立定跳远、掷实心球.测试规定如下:
①三个测试项目中有两项测试成绩合格即可认定为体育达标;
②测试时要求考生先从三个项目中随机抽取两个进行测试,若抽取的两个项目测试都合格或都不合格时,不再参加第三个项目的测试;若抽取的两个项目只有一项合格.则必须参加第三项测试.
已知甲同学跑、跳、掷三个项目测试合格的概率分别是1/2、2/3、3/4,各项测试时间间隔恰当.每次测试互不影响.
(Ⅰ)求甲同学恰好先抽取跳、掷两个项目进行测试的概率;
(Ⅱ)求甲同学经过两个项目测试就能达标的概率;
(Ⅲ)若甲按规定完成测试,参加测试项目个数为X,求X的分布列和期望.