网址:http://m.1010jiajiao.com/timu_id_8742[举报]
说明:对于解题过程中有的题目可用多种解法(或多种证明方法),如果考生的解答与参考答案不同,请参照此评分标准酌情给分.
一. 选择题(本题共10小题,每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
B
D
B
A
D
C
C
评分标准
选对一题给4分,不选,多选,错选均不给分
二、填空题(本题有6小题,每小题5分,共30分)
11.X≠6 ; 12. 2 ; 13.8;
14. 65°;
; 13.8;
14. 65°;
15.96 ; 16. (0,0),(0, ),(0,-3)写对一个给3分,两个4分,三个给5分
),(0,-3)写对一个给3分,两个4分,三个给5分
三、解答题(本题有8小题,共80分)
17. (本题8分)
(1)解:原式=1+3- …………(3分)
…………(3分)
= …………(1分)
…………(1分)
(2)解:愿方程可化为:x=3(x-2 ) …………(2分)
x=3 …………(1分)
经检验 :x=3 是原方程的解. …………(1分)
18.(本题8分)
添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等. ……(2分)
证明例举(以添加条件AD=BC为例):
∵ AB=AB,∠1=∠2,BC=AD, …………(2分)
∴ △ABC≌△BAD. …………(2分)
∴ AC=BD. …………(2分)
19.(本题8分)
(1) ; …………(3分)
; …………(3分)
(2)列对表格或画对树状图; …………(3分)
两次都取到欢欢的概率为 . …………(2分)
. …………(2分)
20.(本题8分)
答案不唯一.只要符合要求,画对一个给4分,画对两个给8分. ……(8分)
21.(本题8分)
(1)∵AB是⊙O直径,∴∠ACB=Rt∠.∴sin∠BAC= . ………(3分)
. ………(3分)
(2)∵OE⊥AC,O是⊙O的圆心, ∴E是AC中点.∴OE= BC=
BC= . …(3分)
. …(3分)
(3)∵AC= =4, ∴tan∠ADC= tan∠ABC=
=4, ∴tan∠ADC= tan∠ABC= .
……(2分)
.
……(2分)
22.(本题10分)
(1) 25 ; ……………(2分)
(2) 50; ……………(2分)
画对条形统计图 ……………(2分)
(3)5人;(列对方程得2分,给出答案给2分) ……………(4分)
23.(本题12分)
(1) ;
………………(2分)
;
………………(2分)
(2)-x2+2x ,1, ; (每格2分)
……………(6分)
; (每格2分)
……………(6分)
(3)设AB长为 m,那么AD为
m,那么AD为
S= ?
? =-
=- . ……………(2分)
. ……………(2分)
当 =
= 时,S最大. ……………(2分)
时,S最大. ……………(2分)
24.(本题14分)
(1)直线AB解析式为:y= x+
x+ .
……………(3分)
.
……………(3分)
(2)方法一:设点C坐标为(x, x+
x+ ),那么OD=x,CD=
),那么OD=x,CD= x+
x+ .
.
∴ =
= =
= .
………(2分)
.
………(2分)
由题意: =
= ,解得
,解得 (舍去) ………(2分)
(舍去) ………(2分)
∴ C(2, ) ………(1分)
) ………(1分)
方法二:∵  ,
, =
= ,∴
,∴ .…(2分)
.…(2分)
由OA= OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD= CD.
CD.
∴  =
= CD×AD=
CD×AD= =
= .可得CD=
.可得CD= . ………(2分)
. ………(2分)
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2, ). ………(1分)
). ………(1分)
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP= OB=3,
OB=3,
∴ (3,
(3, ).
……(2分)
).
……(2分)
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP= OB=1.
OB=1.
∴ (1,
(1, ). …………(1分)
). …………(1分)
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP= OB=
OB= ,OP=
,OP= BP=
BP= .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM= OP=
OP= ;PM=
;PM= OM=
OM= .∴
.∴ (
( ,
, ). ……(1分)
). ……(1分)
 方法二:设P(x ,
方法二:设P(x , x+
x+ ),得OM=x ,PM=
),得OM=x ,PM= x+
x+
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM== =
= ,tan∠ABOC=
,tan∠ABOC= =
= .
.
∴ x+
x+ =
= x,解得x=
x,解得x= .此时,
.此时, (
( ,
, ). ……(1分)
). ……(1分)
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM= OM=
OM= .
.
∴  (
( ,
, )(由对称性也可得到点
)(由对称性也可得到点 的坐标).…………(2分)
的坐标).…………(2分)
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
 (3,
(3, ),
), (1,
(1, ),
), (
( ,
, ),
), (
( ,
, ).
).
注:四个点中,求得一个P点坐标给2分,两个给3分,三个给4分,四个给6分.
(本题14分)如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连结DF,DE, EF. 过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).
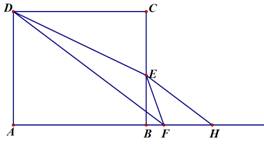
1.(1) 填空:当t= 时,AF=CE,此时BH= ;
2.(2)当△BEF与△BEH相似时,求t的值;
3.(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.
① 求S关于t的函数关系式;
② 直接写出C的最小值.
查看习题详情和答案>>
(本题14分)阅读:在用尺规作线段![]() 等于线段
等于线段![]() 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段![]() .
. ![]()
![]() 求作:线段
求作:线段![]() ,使得线段
,使得线段![]() .
.
作法: ① 作射线![]() ;
;
② 在射线![]() 上截取
上截取![]() .
.
∴线段![]() 为所求.
为所求.
解决下列问题:已知:如图,线段![]() .
. ![]()
(1)请你仿照小明的作法,在上图中的射线![]() 上作线段
上作线段![]() ,使得
,使得![]() ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取![]() 的中点
的中点![]() .若
.若![]() .
.
①当点![]() 在线段
在线段![]() 上时(画出图形)。段
上时(画出图形)。段![]() 的长.
的长.
②当点![]() 在线段
在线段![]() 的延长线上时(画出图形). 求线段
的延长线上时(画出图形). 求线段![]() 的长.
的长.
查看习题详情和答案>>
(本题14分)在同一平面直角坐标系中有6个点![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 的外接圆⊙P,并指出点
的外接圆⊙P,并指出点![]() 与⊙P的位置关系;
与⊙P的位置关系;
(2)若将直线![]() 沿
沿![]() 轴向上平移,当它经过点
轴向上平移,当它经过点![]() 时,设此时的直线为
时,设此时的直线为![]() .
.
①判断直线![]() 与⊙P的位置关系,并说明理由;
与⊙P的位置关系,并说明理由;
②再将直线![]() 绕点
绕点![]() 按顺时针方向旋转,当它经过点
按顺时针方向旋转,当它经过点![]() 时,设此时的直线为
时,设此时的直线为![]() .求直线
.求直线![]() 与⊙P的劣弧
与⊙P的劣弧![]() 围成的图形的面积S(结果保留
围成的图形的面积S(结果保留![]() ).
).

查看习题详情和答案>>
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线![]() 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(![]() ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线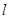 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线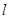 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
查看习题详情和答案>>
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线![]() 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(![]() ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线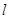 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线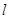 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
查看习题详情和答案>>