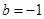摘要:∴取等号条件是. 即 取得最大值.----12分19解法一:
网址:http://m.1010jiajiao.com/timu_id_85592[举报]
已知点 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为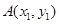 、
、 (其中
(其中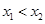 ).
).
(Ⅰ)若 ,求
,求 与
与 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是 ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,
相切,
求圆 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴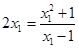 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 ,借助于函数的性质圆
,借助于函数的性质圆 面积的最小值
面积的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴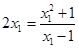 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵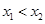 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则 的斜率
的斜率 ,
,
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即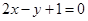 . -----------------7分
. -----------------7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即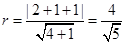 ,--------------8分
,--------------8分
故圆 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ………10分
, ………10分
∴
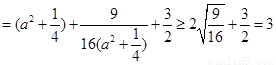 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 .
.
查看习题详情和答案>>
设向量
=(a,b),
=(m,n),其中a,b,m,n∈R,由不等式|
•
|≤|
|•|
|恒成立,可以证明(柯西)不等式(am+bn)2≤(a2+b2)(m2+n2)(当且仅当
∥
,即an=bm时等号成立),己知x,y∈R+,若
+3
<k•
恒成立,利用柯西不等式可求得实数k的取值范围是 .
查看习题详情和答案>>
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| β |
| x |
| y |
| x+y |
已知f(x)=a2x-
x3,x∈(-2,2)为正常数.
(1)可以证明:定理“若a、b∈R*,则
≥
(当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(2)若f(x)>0在(0,2)上恒成立,且函数f(x)的最大值大于1,求实数a的取值范围,并由此猜测y=f(x)的单调性(无需证明);
(3)对满足(2)的条件的一个常数a,设x=x1时,f(x)取得最大值.试构造一个定义在D={x|x>-2,且x≠4k-2,k∈N}上的函数g(x),使当x∈(-2,2)时,g(x)=f(x),当x∈D时,g(x)取得最大值的自变量的值构成以x1为首项的等差数列. 查看习题详情和答案>>
| 1 |
| 2 |
(1)可以证明:定理“若a、b∈R*,则
| a+b |
| 2 |
| ab |
(2)若f(x)>0在(0,2)上恒成立,且函数f(x)的最大值大于1,求实数a的取值范围,并由此猜测y=f(x)的单调性(无需证明);
(3)对满足(2)的条件的一个常数a,设x=x1时,f(x)取得最大值.试构造一个定义在D={x|x>-2,且x≠4k-2,k∈N}上的函数g(x),使当x∈(-2,2)时,g(x)=f(x),当x∈D时,g(x)取得最大值的自变量的值构成以x1为首项的等差数列. 查看习题详情和答案>>
 )上的函数
)上的函数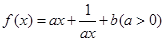
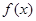 的最小值;
的最小值;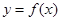 在点
在点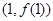 处的切线方程为
处的切线方程为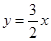 ,求
,求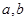 的值。
的值。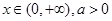 ,故
,故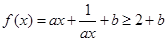 ,取等号的条件是
,取等号的条件是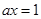 ,即
,即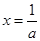 。
。 ,由
,由 ,求得
,求得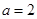 ,又由
,又由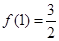 ,可得
,可得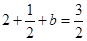 ,解得
,解得