摘要：24． 解: 在抛物线上. ∴ ∴ ∴抛物线的解析式为y=-x2+x+1 C点坐标为(0.1) ∵-×02+×0+1=1 ∴C点在此抛物线上． (3)假设存在这样的点M.使得四边形MCAP的面积最大． ∵△ACP面积为定值. ∴要使四边形MCAP的面积最大.只需使△PCM的面积最大．过点M作MF⊥x轴分别交CP.CB和x轴于E.N和F.过点P作PG⊥x轴交CB于G． =ME?CG=ME 设M(x0.y0).∵∠ECN=30°.CN=x0.∴EN=x0 ∴ME=MF-EF=-x02+x0 ∴=-x02+x ∵a=-<0.∴S有最大值． 当x0=时.S的最大值是. ∵ ∴四边形MCAP的面积的最大值为 此时M点的坐标为(.) 所以存在这样的点M(.).使得四边形MCAP的面积最大.其最大值为．
网址：http://m.1010jiajiao.com/timu_id_8042[举报]
（本题12分）一列快车从甲地驶往乙地，一列慢车从乙地
驶往甲地，两车同时出发，设慢车行驶的时间为
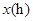，两车之间的距离为
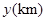，图中的折线表示
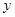与
之间的函数关系．
根据图象进行以下探究：
【小题1】（1）甲、乙两地之间的距离为 
km；
【小题2】（2）请解释图中点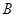
的实际意义；
【小题3】（3）求慢车和快车的速度；
【小题4】（4）求线段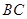
所表示的与之间的函数关系式，并
写出自变量的取值范围；
【小题5】（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？
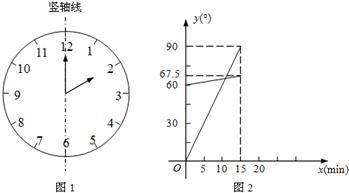
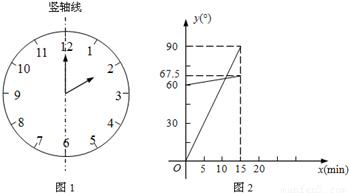
（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2：00～2：15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内的两条线段，在7：30～8：00之间，时针与分针互相垂直的时刻是多少？ 查看习题详情和答案>>
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内的两条线段，在7：30～8：00之间，时针与分针互相垂直的时刻是多少？ 查看习题详情和答案>>
（8分）（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2∶00~2∶15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
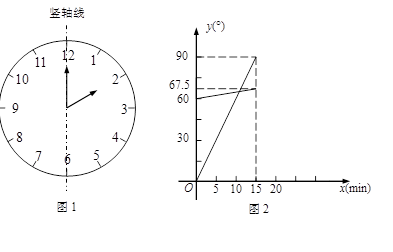
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内
的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？
查看习题详情和答案>>
（8分）（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2∶00~2∶15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内
的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？ 查看习题详情和答案>>
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内
的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？ 查看习题详情和答案>>
（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2：00～2：15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内的两条线段，在7：30～8：00之间，时针与分针互相垂直的时刻是多少？
查看习题详情和答案>>
①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y1°、y2°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y1、y2关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
请你按照小明的思路解决这个问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内的两条线段，在7：30～8：00之间，时针与分针互相垂直的时刻是多少？
查看习题详情和答案>>