题目内容
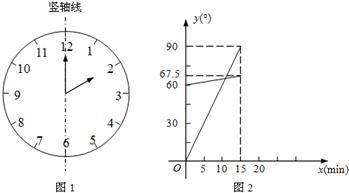
(8分)(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内
的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?
解:(1)时针:y1=60+ x. …………………………………………1分
x. …………………………………………1分
分针:y2=6x. ………………………………………………………………2分
60+ x=6x,解得x=
x=6x,解得x= .…………………………………………………3分
.…………………………………………………3分
所以在2∶00~2∶15之间,时针与分针重合的时刻是2∶10![]() .
.
(注:写2∶![]() 也可.)…………………………………………4分
也可.)…………………………………………4分
(2)方法不惟一.
评分要点:
正确建立函数关系.…………………………………………………………7分
求出时针与分针垂直的时刻是7∶54 . …………………………………8分
. …………………………………8分
(注:没有建立函数关系而直接利用方程求出时针与分针垂直的时刻是7∶54![]() 只得1分.)
只得1分.)
解析:略

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目