摘要:设函数.⑴求的单调区间和极值;⑵是否存在实数,使得关于的不等式的解集为?若存在,求的取值范围;若不存在,试说明理由.说明:本小题主要考查函数的导数.单调性.极值.不等式等基础知识.考查综合利用数学知识分析问题.解决问题的能力.满分14分.解析:(Ⅰ).????????????????????????????????? 2分故当时..时..所以在单调递增.在单调递减.?????????????????????????????????????????????????????? 4分由此知在的极大值为.没有极小值.????????????????????????????????????? 6分当时.由于.故关于的不等式的解集为.???????????????????????????????????????????????????????? 10分(?)当时.由知.其中为正整数.且有.??????????????????????????????????????????????? 12分又时..且.取整数满足..且.则.即当时.关于的不等式的解集不是.综合知.存在.使得关于的不等式的解集为.且的取值范围为. 14分
网址:http://m.1010jiajiao.com/timu_id_80413[举报]
 .
. 的单调区间和极值;
的单调区间和极值; ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ?若存在,求
?若存在,求 .
.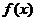 的单调区间和极值;
的单调区间和极值; ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ?若存在,求
?若存在,求