题目内容
设函数 .
.
(Ⅰ)求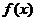 的单调区间和极值;
的单调区间和极值;
(Ⅱ)是否存在实数 ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ?若存在,求
?若存在,求 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
|
【答案】
 .
……2分
.
……2分
故当 时,
时, ,
,  时,
时, .
.
所以, 在
在 单调递增,在
单调递增,在 单调递减.
单调递减.
由此知  在
在 的极大值为
的极大值为 ,没有极小值.
……4分
,没有极小值.
……4分
(Ⅱ)(ⅰ)当 时,
时,
由于 ,
,
故关于 的不等式
的不等式 的解集为
的解集为 ……8分
……8分
(ⅱ)当 时,由
时,由 知
知 =
= ,其中
,其中 为正整数,且有
为正整数,且有 .
……10分
.
……10分
又 时,
时, .
.
且 .
.
取整数 满足
满足 ,
, ,且
,且 ,
,
则 ,
,
即当 时,关于
时,关于 的不等式
的不等式 的解集不是
的解集不是 .
.
综合(ⅰ)(ⅱ)知,存在 ,使得关于
,使得关于 的不等式
的不等式 的解集为
的解集为 ,且
,且 的取值范围为
的取值范围为 .
……12分
.
……12分

练习册系列答案
相关题目
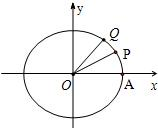 如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且
如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且







 与
与 共线,设函数
共线,设函数 .
. 的周期及最大值;
的周期及最大值;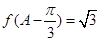 ,边 BC=
,边 BC= ,
, ,求
△ABC 的面积.
,求
△ABC 的面积.