摘要:在直角坐标系中,点到两点的距离之和为4,设点的轨迹为,直线与交于两点.⑴写出的方程;⑵若,求的值;⑶若点在第一象限,证明:当时,恒有.说明:本小题主要考查平面向量.椭圆的定义.标准方程及直线与椭圆位置关系等基础知识.考查综合运用解析几何知识解决问题的能力.满分12分.解析:.由椭圆定义可知.点P的轨迹C是以为焦点.长半轴为2的椭圆.它的短半轴.故曲线C的方程为.??????????????????????????????????????????????????????????????????????????????????? 3分(Ⅱ)设.其坐标满足消去y并整理得.故.??????????????????????????????????????????????????????????????????????? 5分若.即.而.于是.化简得.所以.???????????????????????????????????????????????????????????????????????????? 8分(Ⅲ) .因为A在第一象限.故.由知.从而.又.故.即在题设条件下.恒有.??????????????????????????????????????????????????????????????????????????? 12分
网址:http://m.1010jiajiao.com/timu_id_80411[举报]
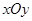 中,点
中,点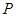 到两点
到两点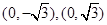 的距离之和等于4,设点
的距离之和等于4,设点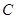 ,直线
,直线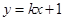 与
与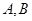 两点.
两点.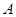 在第一象限,证明当
在第一象限,证明当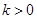 时,恒有
时,恒有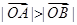 .
.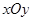 中,点
中,点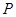 到两点
到两点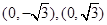 的距离之和等于4,设点
的距离之和等于4,设点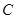 ,直线
,直线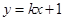 与
与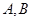 两点.
两点.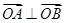 ,求
,求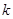 的值.
的值. 中,点
中,点 到两点
到两点 的距离之和为4,设点
的距离之和为4,设点 ,直线
,直线 与
与 两点.
两点. ,求
,求 的值
的值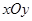 中,点
中,点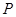 到两点
到两点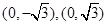 的距离之和等于4,设点
的距离之和等于4,设点 ,直线
,直线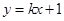 与
与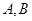 两点.
两点.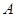 在第一象限,证明当
在第一象限,证明当 时,恒有
时,恒有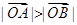 .
.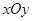 中,点
中,点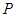 到两点
到两点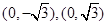 的距离之和等于4,设点
的距离之和等于4,设点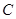 ,直线
,直线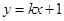 与
与 两点.
两点.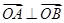 ,求
,求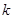 的值.
的值.