摘要：=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4???????????????????????????????? 12分 ⑴证明:平面和平面互相垂直;⑵证明:截面和截面面积之和是定值,并求出这个值;⑶若与平面所成的角为,求与平面所成角的正弦值.说明:本小题主要考查空间中的线面关系.面面关系.解三角形等基础知识.考查空间想象能力与逻辑思维能力.满分12分．解法一:(Ⅰ)证明:在正方体中...又由已知可得 所以..所以平面．所以平面和平面互相垂直．???????????????????????? 4分知.又截面PQEF和截面PQGH都是矩形.且PQ=1.所以截面PQEF和截面PQGH面积之和是.是定值．?????????????????????????????????????????????????????????????????????? 8分(III)解:连结BC′交EQ于点M．因为..所以平面和平面PQGH互相平行.因此与平面PQGH所成角与与平面所成角相等．与(Ⅰ)同理可证EQ⊥平面PQGH.可知EM⊥平面.因此EM与的比值就是所求的正弦值．设交PF于点N.连结EN.由知．因为⊥平面PQEF.又已知与平面PQEF成角.所以.即.解得.可知E为BC中点．所以EM=.又.故与平面PQCH所成角的正弦值为．????????????????????????????????????????????????? 12分解法二:以D为原点.射线DA.DC.DD′分别为x.y.z轴的正半轴建立如图的空间直角坐标系D-xyz由已知得.故 .....．(Ⅰ)证明:在所建立的坐标系中.可得..．因为.所以是平面PQEF的法向量．因为.所以是平面PQGH的法向量．因为.所以.所以平面PQEF和平面PQGH互相垂直．????????????????????????????????????????????????????????????????????? 4分(Ⅱ)证明:因为.所以.又.所以PQEF为矩形.同理PQGH为矩形．在所建立的坐标系中可求得..所以.又.所以截面PQEF和截面PQGH面积之和为.是定值．????????????????????????????????????????????? 8分(Ⅲ)解:由已知得与成角.又可得 .即.解得．所以.又.所以与平面PQGH所成角的正弦值为．????????????????????????????????????????????????????????????????????????? 12分
网址：http://m.1010jiajiao.com/timu_id_80410[举报]
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”．为提高公众对健康睡眠的科学认识和自我管理能力，某网站于3月13日起进行了为期一周的在线调查，共有200人参与．现将数据整理分组如表所示．（1）画出频率分布直方图；
（2）调查对象中睡眠时间少于8的频率是多少？
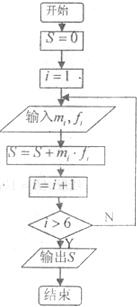
（3）为了对数据进行分析，采用了计算机辅助计算，算法流程如图所示．求输出的S的值，并说明S的统计意义．
| 序号i | 分组睡眠时间（小时） | 组中值（m1） | 频数（人数） | 频率（f1） |
| 1 | [4，5） | 4.5 | 8 | 0.04 |
| 2 | [5，6） | 5.5 | 52 | 0.26 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.28 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10） | 9.5 | 4 | 0.02 |
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识，为此某网站进行了持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．
（1）在答题卡给定的坐标系中画出频率分布直方图；
（2）睡眠时间小于8的概率是多少？
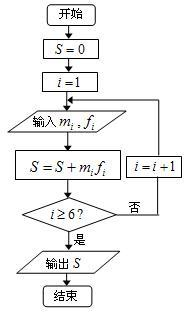
（3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
查看习题详情和答案>>
| 序号（i） | 分组睡眠时间 | 组中值（mi） | 频数 （人数） |
频率 （fi） |
| 1 | [4，5） | 4.5 | 8 | 0.04 |
| 2 | [5，6） | 5.5 | 52 | 0.26 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.28 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10] | 9.5 | 4 | 0.02 |
（1）在答题卡给定的坐标系中画出频率分布直方图；
（2）睡眠时间小于8的概率是多少？
（3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
“世界睡眠日”定在每年的3月21日．2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站2009年3月13日到3月20日持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图，则输出的S值为6
6
，S的统计意义是70
70
．| 序号 （i） |
分组 睡眠时间 |
组中值 （mi） |
频数 （人数） |
频率 （fi） |
| 1 | [4，5） | 4.5 | 8 | 0.04 |
| 2 | [5，6） | 5.5 | 52 | 0.26 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.28 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10] | 9.5 | 4 | 0.02 |
国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：
| 序号( | 每天睡眠时间 （小时） | 组中值( | 频数 | 频率 ( |
| 1 | [4，5) | 4.5 | 8 | 0.04 |
| 2 | [5，6) | 5.5 | 52 | 0.26 |
| 3 | [6，7) | 6.5 | 60 | 0.30 |
| 4 | [7，8) | 7.5 | 56 | 0.28 |
| 5 | [8，9) | 8.5 | 20 | 0.10 |
| 6 | [9，10) | 9.5 | 4 | 0.02 |
)
)
)
 |
（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；
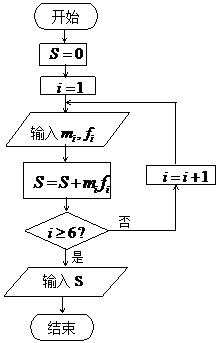
（Ⅱ）该网站利用上面的算法流程图，对样本数据作进一步统计
分析，求输出的S的值，并说明S的统计意义.
查看习题详情和答案>>(本小题满分12分)
国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：
| 序号( | 每天睡眠时间 （小时） | 组中值( | 频数 | 频率 ( |
| 1 | [4，5) | 4.5 | 8 | 0.04 |
| 2 | [5，6) | 5.5 | 52 | 0.26 |
| 3 | [6，7) | 6.5 | 60 | 0.30 |
| 4 | [7，8) | 7.5 | 56 | 0.28 |
| 5 | [8，9) | 8.5 | 20 | 0.10 |
| 6 | [9，10) | 9.5 | 4 | 0.02 |
)
)
)（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；
（Ⅱ）该网站利用右边的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义.
 |
查看习题详情和答案>>